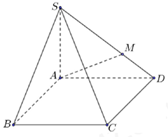
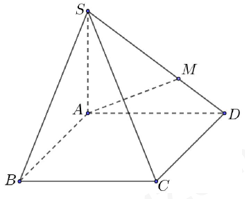
Cho hình chóp \(S.ABC{\rm{D}}\) có đáy \(ABC{\rm{D}}\) là hình bình hành. Gọi điểm \(M\) là điểm thuộc cạnh \(S{\rm{D}}\) sao cho \(SM = \dfrac{2}{3}SD\) (minh họa như hình vẽ). Mặt phẳng chứa \(AM\) và song song với \(B{\rm{D}}\) cắt cạnh \(SC\) tại \(K\). Tỷ số \(\dfrac{{SK}}{{SC}}\) bằng
Trả lời bởi giáo viên
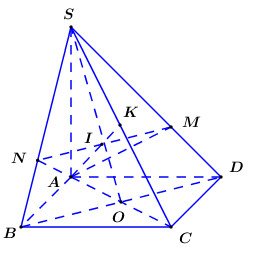
Gọi mặt phẳng chứa \(AM\) và song song với \(BD\) là \(\left( \alpha \right)\).
Trong \(\left( {SBD} \right)\) kẻ \(MN//BD\,\,\left( {N \in SB} \right)\), khi đó ta có \(\left( \alpha \right) \equiv \left( {AMN} \right)\).
Gọi \(O = AC \cap BD\), trong \(\left( {SBD} \right)\) gọi \(\left\{ I \right\} = MN \cap SO\), trong \(\left( {SAC} \right)\) gọi \(K = AI \cap SC\) ta có:
\(\left\{ \begin{array}{l}K \in AI \subset \left( {AMN} \right)\\K \in SC\end{array} \right.\)\( \Rightarrow K = \left( {AMN} \right) \cap SC\) hay \(K = \left( \alpha \right) \cap SC\).
Áp dụng định lí Talets ta có \(\dfrac{{SI}}{{SO}} = \dfrac{{SM}}{{SD}} = \dfrac{2}{3}\).
\( \Rightarrow \dfrac{{IS}}{{IO}}=2\)
Ta có: O là trung điểm của AC nên \(\dfrac{{AO}}{{AC}}=\dfrac{1}{2}\)
Áp dụng định lí Menelaus trong tam giác \(SOC\), cát tuyến \(AIK\) ta có:
\(\dfrac{{IS}}{{IO}}.\dfrac{{AO}}{{AC}}.\dfrac{{KC}}{{KS}} = 1 \Leftrightarrow 2.\dfrac{1}{2}.\dfrac{{KC}}{{KS}} = 1 \Leftrightarrow \dfrac{{KC}}{{KS}} = 1\) \( \Rightarrow \dfrac{{SK}}{{SC}} = \dfrac{1}{2}\).
Hướng dẫn giải:
- Xác định điểm \(K\).
- Sử dụng định lí Talets và định lí Menelaus trong tam giác \(SOC\) để tính tỉ số.
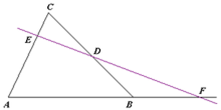
Định lý Menelaus: Cho tam giác ABC. D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB. Khi đó định lý phát biểu rằng D, E, F thẳng hàng khi và chỉ khi
\(\dfrac{{FA}}{{FB}}.\dfrac{{DB}}{{DC}}.\dfrac{{EC}}{{EA}} = 1\)
Câu hỏi khác
- Đề thi tư duy định lượng - Đề số 1 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 2 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 4 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 11 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 5 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
