Trong không gian với hệ tọa độ Oxyz cho điểm \(A( - 2;2; - 2)\) và điểm \(B(3; - 3;3)\). Điểm \(M\) thay đổi trong không gian thỏa mãn \(\dfrac{{MA}}{{MB}} = \dfrac{2}{3}\). Điểm \(N(a;b;c)\) thuộc mặt phẳng \((P): - x + 2y - 2z + 6 = 0\) sao cho MN nhỏ nhất. Tính tổng \(T = a + b + c\).
Trả lời bởi giáo viên
Bước 1: Gọi \(M(x;y;z)\). Tìm quỹ tích của M
Gọi \(M(x;y;z)\). Ta có \(\dfrac{{MA}}{{MB}} = \dfrac{2}{3}\)
\( \Leftrightarrow 9M{A^2} = 4M{B^2} \Leftrightarrow {(x + 6)^2} + {(y - 6)^2} + {(z + 6)^2} = 108\).
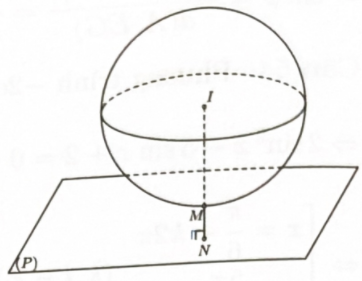
Vây điểm \(M\) thuộc mặt cầu tâm \(I( - 6;6; - 6)\), bán kính \(R = 6\sqrt 3 \).
Vậy MN nhỏ nhất khi M, N thuộc đường thẳng đi qua tâm \(I\) và vuông góc với mặt phẳng (P).
Bước 2: Tìm điểm N và tính T.
Gọi \((d)\) là đường thẳng đi qua tâm \(I\) và vuông góc với mặt phẳng (P).
Khi đó \((d):\left\{ {\begin{array}{*{20}{l}}{x = - 6 - t}\\{y = 6 + 2t}\\{z = - 6 - 2t}\end{array}} \right.\).
Tọa độ điểm \(N\) là nghiệm của hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x = - 6 - t}\\{y = 6 + 2t}\\{z = - 6 - 2t}\\{ - x + 2y - 2z + 6 = 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = - 6 - t\\y = 6 + 2t\\z = - 6 - 2t\\6 + t + 12 + 4t + 12 + 4t + 6 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - 2}\\{y = - 2}\\{z = 2}\\{t = - 4}\end{array}} \right.\)
\( \Rightarrow N\left( { - 2; - 2;2} \right)\)
Do đó \(T = - 2 - 2 + 2 = - 2\)
Hướng dẫn giải:
Bước 1: Gọi \(M(x;y;z)\). Tìm quỹ tích của M
Bước 2: Gọi \((d)\) là đường thẳng đi qua tâm \(I\) và vuông góc với mặt phẳng (P). Tìm điểm N và tính T.
Câu hỏi khác
- Đề thi tư duy định lượng - Đề số 1 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 2 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 4 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 11 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
- Đề thi tư duy định lượng - Đề số 5 đánh giá năng lực ĐHQG Hà Nội có lời giải chi tiết
