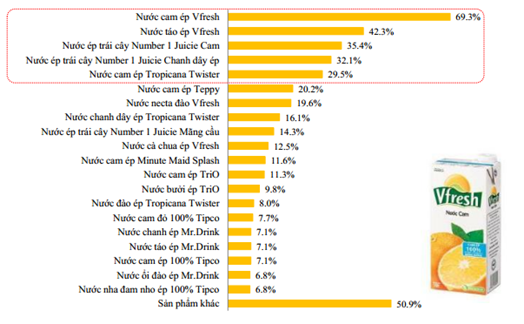
Biết rằng \(z\) là số phức có môđun nhỏ nhất thỏa mãn \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) là số thực. Số phức \(z\) là:
Trả lời bởi giáo viên
Cách 1:
Gọi \(z = x + yi\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\), theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\left( {1 - z} \right)\left( {\bar z + 2i} \right)\\ = \left( {1 - x - yi} \right)\left( {x - yi + 2i} \right)\\ = \left( {1 - x - yi} \right)\left( {x - \left( {y - 2} \right)i} \right)\\ = \left( {1 - x} \right)x - \left( {1 - x} \right)\left( {y - 2} \right)i - xyi - y\left( {y - 2} \right)\\ = \left[ {\left( {1 - x} \right)x - y\left( {y - 2} \right)} \right] - \left[ {\left( {1 - x} \right)\left( {y - 2} \right) + xy} \right]i\end{array}\)
Để \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) là số thực thì \({\mathop{\rm Im}\nolimits} \left( {1 - z} \right)\left( {\bar z + 2i} \right) = 0\)
\(\begin{array}{l} \Leftrightarrow \left( {1 - x} \right)\left( {y - 2} \right) + xy = 0\\ \Leftrightarrow y - 2 - xy + 2x + xy = 0\\ \Leftrightarrow y = 2 - 2x\end{array}\)
Khi đó ta có: \({\left| z \right|^2} = {x^2} + {y^2} = {x^2} + {\left( {2 - 2x} \right)^2} = 5{x^2} - 8x + 4\).
\( \Rightarrow {\left| z \right|_{\min }} \Leftrightarrow {\left| z \right|^2}_{\min } \Leftrightarrow x = \dfrac{8}{{2.5}} = \dfrac{4}{5}\), khi đó \(y = 2 - 2.\dfrac{4}{5} = \dfrac{2}{5}\).
Vậy số phức \(z\) thỏa mãn yêu cầu bài toán là: .\(z = \dfrac{4}{5} + \dfrac{2}{5}i\).
Hướng dẫn giải:
Cách 1:
- Đặt \(z = x + yi\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\), thay vào biểu thức \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\), tìm điều kiện để \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) là số thực, tức là \({\mathop{\rm Im}\nolimits} \left( {1 - z} \right)\left( {\bar z + 2i} \right) = 0\), biểu diễn \(y\) theo \(x\).
- Tính \(\left| z \right| = \sqrt {{x^2} + {y^2}} \), thế \(y\) theo \(x\) tìm được ở trên, tìm GTNN của biểu thức dạng \(a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\), biểu thức đạt GTNN tại \(x = - \dfrac{b}{{2a}}\) với \(a > 0\).
Cách 2:
- Tính môđun cả 4 số phức ở 4 đáp án, thử từ số phức có môđun nhỏ nhất.
- Thay lần lượt các số phức ở các đáp án vào biểu thức \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\), tìm số phức thỏa mãn \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) là số thực.
Giải thích thêm:
Cách 2:
Tính môđun tất cả các số phức ở các đáp án:
\(z = 1 + \dfrac{1}{2}i \Rightarrow \left| z \right| = \dfrac{{\sqrt 5 }}{2}\)
\(z = \dfrac{3}{5} + \dfrac{4}{5}i \Rightarrow \left| z \right| = 1\)
\(z = 2i \Rightarrow \left| z \right| = 2\)
\(z = \dfrac{4}{5} + \dfrac{2}{5}i \Rightarrow \left| z \right| = \dfrac{{2\sqrt 5 }}{5}\).
Thử từ số phức có môđun nhỏ nhất.
Nhập vào màn hình như sau:
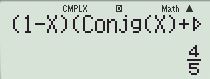
Xét đáp án D, thay số phức \(z = \dfrac{4}{5} + \dfrac{2}{5}i\) vào biểu thức \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) (đã nhập trên máy tính) ta thấy kết quả là số thực, thỏa mãn.
Vậy số phức \(z = \dfrac{4}{5} + \dfrac{2}{5}i\) thỏa mãn yêu cầu bài toán.
Cách bấm máy tính:
MODE 2
Nhập: (1- ALPHA X)( SHIFT 2 2 ALPHA X)+2 SHIFT \(i\) )
Bấm CALC 4:5 + 2:5 SHIFT \(i\) =
Hiện ra kết quả $\frac{4}{5}$ nên là số thực, thỏa mãn bài toán.