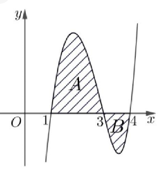
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Biết các miền \(A\) và \(B\) có diện tích lần lượt là 4 và 1. Tính \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)

Đáp án: \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)

Các hành vi không khai báo, khai báo không trung thực hoặc che giấu hiện trạng bệnh của bản thân hoặc người khác mắc bệnh truyền nhiễm nhóm A đều bị xử phạt theo quy định của pháp luật.

Hành vi nào sau đây có mực xử phạt hành chính cao nhất:

Một chất điểm chuyển động theo phương trình \(S =  - \dfrac{1}{3}{t^3} + 6{t^2}\), trong đó \(t > 0,t\) được tính bằng giây \((s)\) và \(S\) tính bằng mét \((m)\). Vận tốc của chất điểm tại thời điểm \(t = 3\) (giây) bằng

Tìm tập nghiệm của phương trình  \({\log _3}x + \dfrac{1}{{{{\log }_9}x}} = 3\)

Hệ \(\left\{ \begin{array}{l}x - y = 5\\{x^2} - {y^2} = 15\end{array} \right.\) có nghiệm là

Gọi \(A\) và \(B\) lần lượt là điểm biểu diễn của số phức \({z_1} = 3 - 2i\) và \({z_2} = 1 + 4i\). Trung điểm của đoạn thẳng \(AB\) có tọa độ là:

Trong không gian với hệ trục tọa độ \({\mathop{\rm Oxyz}\nolimits} \), cho điểm \(A(4; - 3;5)\) và \(B(2; - 5;1).\)Viết phương trình mặt phẳng \((P)\) đi qua trung điểm \(I\) của đoạn thẳng \(AB\) và vuông góc với đường thẳng \((d):\dfrac{{x + 1}}{3} = \dfrac{{y - 5}}{{ - 2}} = \dfrac{{z + 9}}{{13}}\).

Khi chiếu điểm \(M\left( { - 4;3; - 2} \right)\) lên trục ${\rm{Ox}}$ được điểm \(N\) thì: