Trong không gian \(Oxyz,\) cho hai điểm \(A\left( {4;0;4} \right)\) và \(B\left( {2;4;0} \right)\). Điểm \(M\) di động trên tia \(Oz\), điểm \(N\) di động trên tia \(Oy\). Đường gấp khúc \(AMNB\) có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục).
Trả lời bởi giáo viên
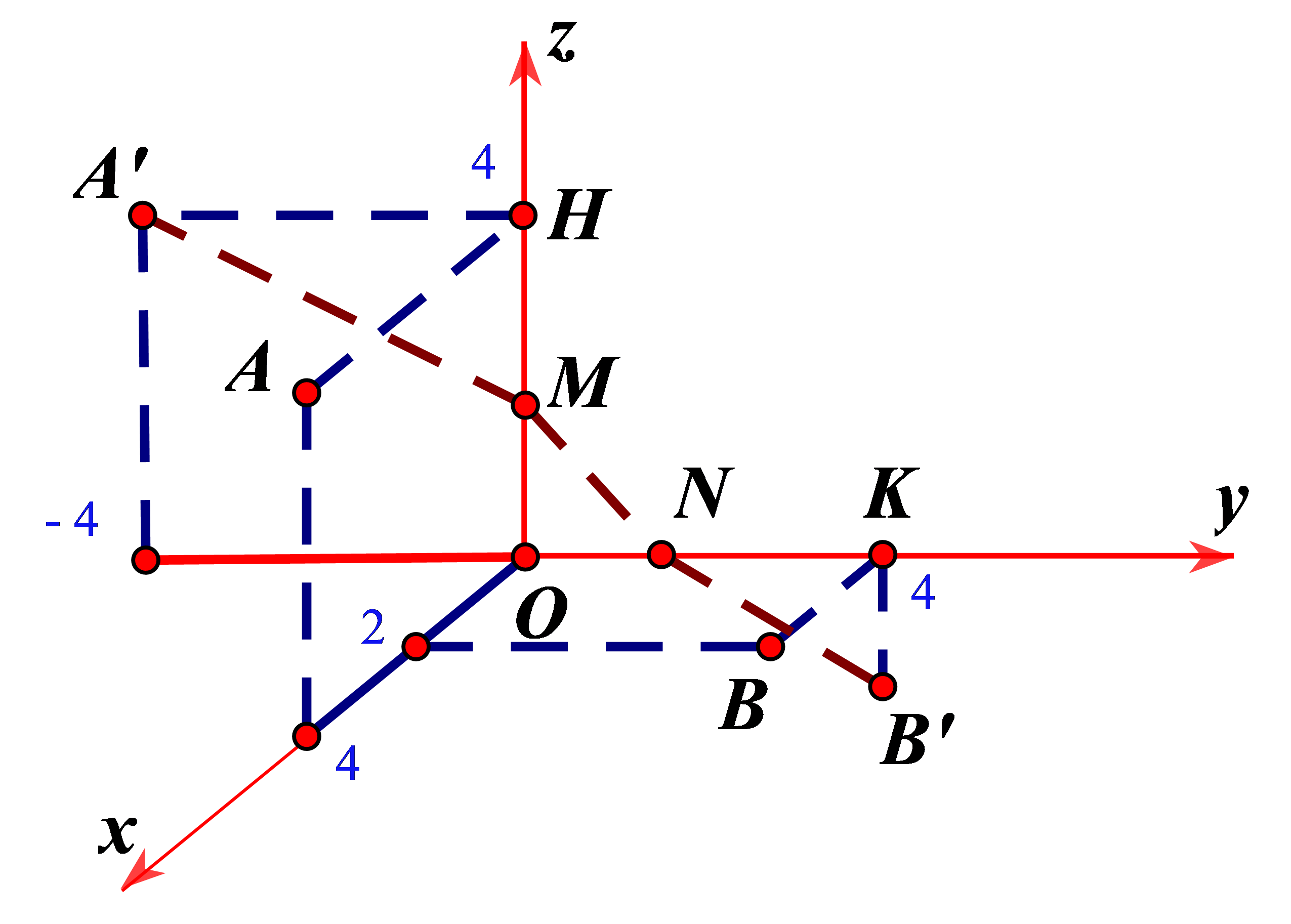
Ta có \(H\left( {0;0;4} \right)\) và \(K\left( {0;4;0} \right)\) là hình chiếu của \(A\) trên \(Oz\) và \(B\) trên \(Oy\)
Gọi \(A'\left( {0; - 4;4} \right);B'\left( {0;4; - 2} \right)\).
Xét hai tam giác vuông \(AHM;AHA'\) có chung\(HM;\,\,HA = HA' = 4 \Rightarrow \Delta AHM = \Delta A'HM\) (2 cạnh góc vuông) \( \Rightarrow AM = A'M\)
Chứng minh tương tự ta có \(BN = B'N\) .
Độ dài đường gấp khúc \(AMNB\) là \(AM + MN + NB = A'M + MN + NB' \ge A'B' = 10\).
(Lưu ý rằng các điểm \(A',M,N,B'\) cùng nằm trên mặt phẳng \(Oyz\)).
Hướng dẫn giải:
- Gọi \(H,\,\,K\) là hình chiếu của \(A\) trên \(Oz\) và \(B\) trên \(Oy\).
- Gọi \(A'\left( {0; - 4;4} \right);B'\left( {0;4; - 2} \right)\). Chứng minh \(AM = A'M\), \(BN = B'N\).
- Độ dài đường gấp khúc \(AMNB\) là \(AM + MN + NB = A'M + MN + NB' \ge A'B'\).


