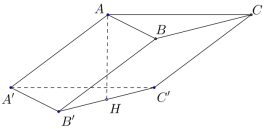
Cho hình lăng trụ \(ABC.A'B'C'\) có tam giác \(ABC\) vuông tại \(A\), \(AB = a\), \(AC = a\sqrt 3 \), \(AA' = 2a\). Hình chiếu vuông góc của điểm \(A\) trên mặt phẳng \(\left( {A'B'C'} \right)\) trùng với trung điểm \(H\) của đoạn \(B'C'\) (tham khảo hình vẽ dưới đây). Khoảng cách giữa hai đường thẳng \(AA'\) và \(BC'\) bằng \(\dfrac{{a\sqrt {m} }}{5}\). Tìm $m$.

Đáp án:

Bước 1:

Ta có \(AA'//BB' \Rightarrow AA'//\left( {BCC'B'} \right) \supset BC'\) \( \Rightarrow d\left( {AA';BC'} \right) = d\left( {AA';\left( {BCC'B'} \right)} \right) = d\left( {A;\left( {BCC'B'} \right)} \right)\).

Bước 2:

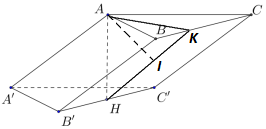
Trong \(\left( {ABC} \right)\) kẻ \(AK \bot BC\,\,\left( {K \in BC} \right)\), trong \(\left( {AHK} \right)\) kẻ \(AI \bot HK\,\,\left( {I \in HK} \right)\) ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AK\\BC \bot AH\end{array} \right. \Rightarrow BC \bot \left( {AHK} \right) \Rightarrow BC \bot AI\\\left\{ \begin{array}{l}AI \bot HK\\AI \bot BC\end{array} \right. \Rightarrow AI \bot \left( {BCC'B'} \right)\end{array}\)

\( \Rightarrow d\left( {A;\left( {BCC'B'} \right)} \right) = AI = d\left( {AA';BC'} \right)\).

Bước 3:

Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) ta có \(AK = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{a.a\sqrt 3 }}{{\sqrt {{a^2} + 3{a^2}} }} = \dfrac{{a\sqrt 3 }}{2}\).

Tam giác \(A'B'C'\) có \(B'C' = \sqrt {A'B{'^2} + A'C{'^2}}  = 2a\) \( \Rightarrow A'H = \dfrac{1}{2}B'C' = a\).

\( \Rightarrow AH = \sqrt {AA{'^2} - A'{H^2}}  = \sqrt {4{a^2} - {a^2}}  = a\sqrt 3 \).

Áp dụng hệ thức lượng trong tam giác vuông \(AHK\) ta có \(AI = \dfrac{{AH.AK}}{{\sqrt {A{H^2} + A{K^2}} }} = \dfrac{{a\sqrt 3 .\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {3{a^2} + \dfrac{{3{a^2}}}{4}} }} = \dfrac{{a\sqrt {15} }}{5}\).

Vậy \(d\left( {AA';BC'} \right) = \dfrac{{a\sqrt {15} }}{5}\).

Vậy $m=15$.