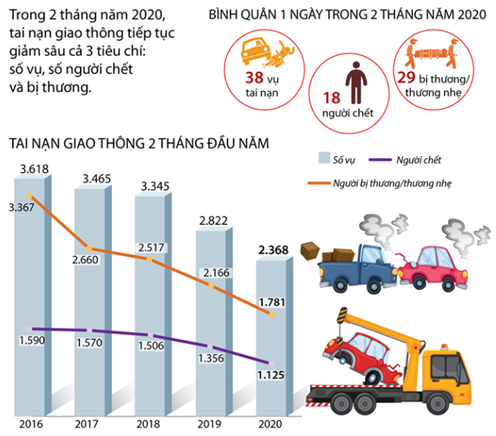
Gọi $(H)$ là tập hợp các điểm biểu diễn số phức $z$ thỏa mãn $1 \leq|z-1| \leq 2$ trong mặt phẳng phức. Khi đó, diện tích hình $(H)$ bằng
Trả lời bởi giáo viên
$3 \pi$
Bước 1: Đặt $z=x+yi$, biểu diên |z-1| theo x và y.
Đặt $z=x+y i,|z-1|=|x-1+y i|=\sqrt{(x-1)^{2}+y^{2}}$
Bước 2: Đánh giá |z-1| từ đó tìm tập hợp điểm biểu diễn z và tính diện tích hình phẳng S.
Do đó
\(\begin{array}{l}1 \le |z - 1| \le 2\\ \Leftrightarrow 1 \le \sqrt {{{(x - 1)}^2} + {y^2}} \le 2\\ \Leftrightarrow 1 \le {(x - 1)^2} + {y^2} \le 4\end{array}\)
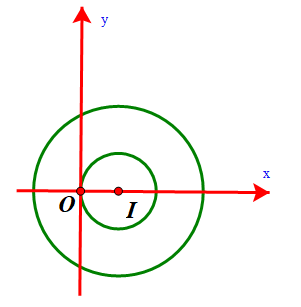
Tập hợp các điểm biểu diễn số phức $z$ là hình phẳng nằm trong đường tròn tâm $I(1 ; 0)$ bán kính $R=2$ và nằm ngoài đường tròn $I(1 ; 0)$ bán kính $r=1$
Diện tích hình phẳng $S=\pi \cdot 2^{2}-\pi \cdot 1^{2}=3 \pi$
Hướng dẫn giải:
Bước 1: Đặt $z=x+y i, biểu diên |z-1| theo x và y.
Bước 2: Đánh giá |z-1| từ đó tìm tập hợp điểm biểu diễn z và tính diện tích hình phẳng S.