I. Vị trí tương đối giữa mặt phẳng và mặt cầu
Cho mặt phẳng (P) và mặt cầu (S) tâm I bán kính R. Khi đó:
- (S)∩(P)=∅⇔d(I,(P))>R.
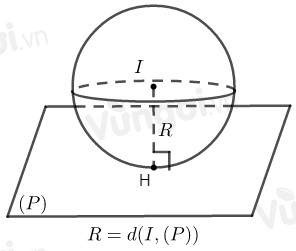
- (S)∩(P)={H}⇔d(I,(P))=R.
ở đó, H là tiếp điểm, (P) là tiếp diện và OH⊥(P) tại H.
- (S)∩(P)=C(H;r)⇔d(I,(P))<R.
ở đó : với H là hình chiếu của I trên (P).
Đặc biệt: d(I,(P))=0 hay (P) đi qua I thì (S)∩(P)=C(I;R).
C(I;R) được gọi là đường tròn lớn, (P) là mặt phẳng kính.
II. Viết phương trình mặt cầu tiếp xúc hoặc cắt mặt phẳng cho trước.
Phương pháp:
- Bước 1: Tính bán kính mặt cầu dựa vào các điều kiện bài cho:
+ Tiếp xúc mặt phẳng nếu d(I,(P))=R
+ Cắt mặt phẳng theo giao tuyến và đường tròn bán kính r thì R2=r2+d2(I,(P))

- Bước 2: Viết phương trình mặt cầu biết tâm và bán kính.
III. Viết phương trình mặt phẳng tiếp xúc, giao với mặt cầu cho trước
Phương pháp:
- Bước 1: Tìm VTPT của mặt phẳng (P) dựa vào điều kiện bài cho.
+ Tiếp xúc mặt cầu tại điểm H thì →nP=→IH
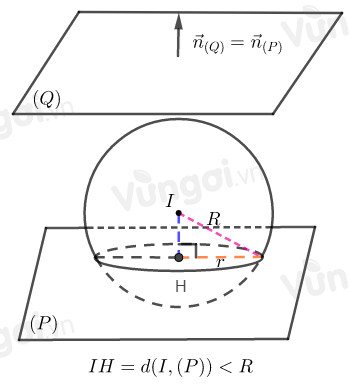
+ Trường hợp (P) song song với mặt phẳng (Q):ax+by+cz+d=0 (a,b,c,d là các số cho trước) và cắt mặt cầu theo đường tròn có bán kính r thì →nP=→nQ tức là (P):ax+by+cz+d′=0.
và d(I,(P))=√R2−r2.
- Bước 2: Viết phương trình mặt phẳng.
+ Tiếp xúc mặt cầu tại điểm H: Xác định điểm H rồi lập phương trình mặt phẳng.
+ Trường hợp (P) song song với mặt phẳng (Q):ax+by+cz+d=0 (a,b,c,d là các số cho trước) và cắt mặt cầu theo đường tròn có bán kính r:
Sử dụng d(I,(P))=√R2−r2 để tìm d'.

