I. Vị trí tương đối của đường thẳng và mặt phẳng
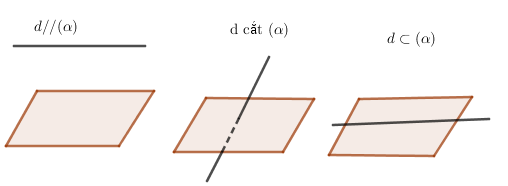
Cho đường thẳng \(d\) và mặt phẳng \(\left( \alpha \right)\), ta có ba vị trí tương đối giữa chúng là:
- \(d//\left( \alpha \right)\) nếu \(d\) và \(\left( \alpha \right)\) không có điểm chung.
- \(d \subset \left( \alpha \right)\) nếu mọi điểm nằm trong \(d\) đều nằm trong \(\left( \alpha \right)\).
- \(d\) cắt \(\left( \alpha \right)\) nếu \(d\) và \(\left( \alpha \right)\) có duy nhất một điểm chung.
II. Các định lý và tính chất
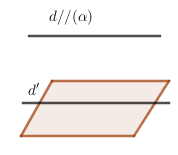
Định lý 1: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \(\left( \alpha \right)\) mà \(d\) song song với một đường thẳng \(d'\) nằm trong \(\left( \alpha \right)\) thì \(d\) song song với \(\left( \alpha \right)\).
Vậy \(\left\{ \begin{array}{l}d \not\subset \left( \alpha \right)\\d//d'\\d' \subset \left( \alpha \right)\end{array} \right. \Rightarrow d//\left( \alpha \right)\)
Định lý 2: Cho đường thẳng \(d\) song song với mặt phẳng \(\left( \alpha \right)\), nếu mặt phẳng \(\left( \beta \right)\) chứa \(d\) mà cắt \(\left( \alpha \right)\) theo giao tuyến \(d'\) thì \(d//d'\).
Vậy \(\left\{ \begin{array}{l}d//\left( \alpha \right)\\\left( \beta \right) \cap \left( \alpha \right) = d'\\d \subset \left( \beta \right)\end{array} \right. \Rightarrow d//d'\)
Định lý 3: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
Vậy \(\left\{ \begin{array}{l}d//\left( \alpha \right)\\d//\left( \beta \right)\\\left( \alpha \right) \cap \left( \beta \right) = d'\end{array} \right. \Rightarrow d//d'\).
Định lý 4: Cho hai đường thẳng chéo nhau, có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
III. Chứng minh đường thẳng song song với mặt phẳng
Phương pháp:
Cách 1: Tìm một đường thẳng thuộc mặt phẳng mà song song với đường thẳng đã cho.
Cách 2: Chứng minh đường thẳng đó là giao của hai mặt phẳng mà lần lượt cắt mặt phẳng đã cho theo hai giao tuyến song song.
Ví dụ: Cho hình chóp \(S.ABC\) có \({G_1},{G_2}\) lần lượt là trọng tâm các tam giác \(SBC,ABC\). Chứng minh \({G_1}{G_2}//\left( {SAC} \right)\)
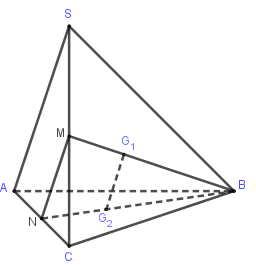
Gọi \(M,N\) lần lượt là trung điểm của \(SC,AC\).
Khi đó \(\dfrac{{B{G_1}}}{{BM}} = \dfrac{{B{G_2}}}{{BN}} = \dfrac{2}{3} \Leftrightarrow {G_1}{G_2}//MN\)
Mà \(M \in SC,N \in AC\) nên \(MN \subset \left( {SAC} \right)\)
Vậy \({G_1}{G_2}//\left( {SAC} \right)\)
