I. Vị trí tương đối giữa hai đường thẳng
Cho d,d′ là các đường thẳng có VTCP lần lượt là →u,→u′,M∈d,M′∈d′ . Ta có:
+) d≡d′⇔→u,→u′,→MM′ đôi một cùng phương ⇔[→u,→u′]=[→u,→MM′]=→0
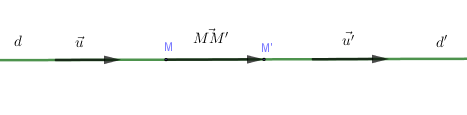
+) d//d′⇔→u,→u′ cùng phương nhưng →u,→MM′ không cùng phương ⇔{[→u,→u′]=→0[→u,→MM′]≠→0
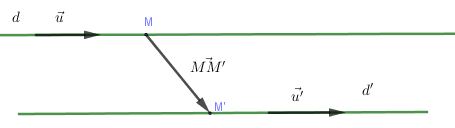
+) d cắt d′⇔→u,→u′ không cùng phương và →u,→u′,→MM′ đồng phẳng ⇔{[→u,→u′]≠→0[→u,→u′]→MM′=0
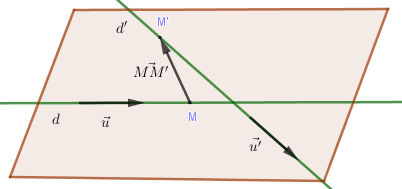
+) d chéo d′⇔→u,→u′,→MM′ không đồng phẳng ⇔[→u,→u′]→MM′≠0
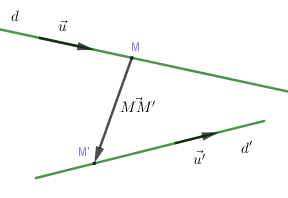
Ngoài ra, ta có thể giải hệ phương trình của hai đường thẳng để xét vị trí tương đối của hai đường thẳng:
+) Nếu hệ có nghiệm duy nhất thì d cắt d′.
+) Nếu hệ vô số nghiệm thì d≡d′.
+) Nếu hệ vô nghiệm thì:
d//d′ nếu →u=k→u′ hay →u,→u′ cùng phương.
d chéo d′ nếu →u≠k→u′ hay →u,→u′ không cùng phương.
II. Khoảng cách và góc
a) Khoảng cách từ điểm A đến đường thẳng d′
d(A,d′)=SANN′M′AN=|[→AM′,→u′]||→u′|
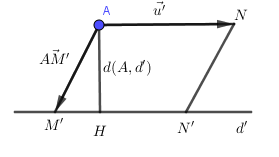
b) Khoảng cách giữa hai đường thẳng:
d(Δ,Δ′)=|[→u,→u′].→MM′||[→u,→u′]|
c) Góc giữa hai đường thẳng có các VTCP lần lượt là: →u,→u′:
cosφ=|cos(→u,→u′)|=|→u.→u′||→u|.|→u′|

