I. Hàm số lũy thừa
Định nghĩa:
- Hàm số lũy thừa là hàm số có dạng y=xα(α∈R).
- Tập xác định:
+ α nguyên dương: D=R.
+ α nguyên âm hoặc α=0: D=R∖{0}.
+ α không nguyên: D=(0;+∞).
Chú ý:
n√x=x1n⇔x>0. Ngoài ra hai hàm số y=n√x và y=x1n(n∈N∗) là không đồng nhất vì có tập xác định khác nhau.
Đạo hàm:
(xα)′=αxα−1;uα(x)′=αu′(x)uα−1(x)
(n√x)′=1nn√xn−1;(n√u(x))′=u′(x)nn√un−1(x)
+ Nếu x>0 thì n√x=x1n nên (n√x)′=(x1n)′=1nx−n−1n=1nn√xn−1
+ Nếu x≤0 thì đẳng thức trên không xảy ra.
Sự biến thiên:
Khảo sát hàm số y=xα(α≠0) trên tập (0;+∞).
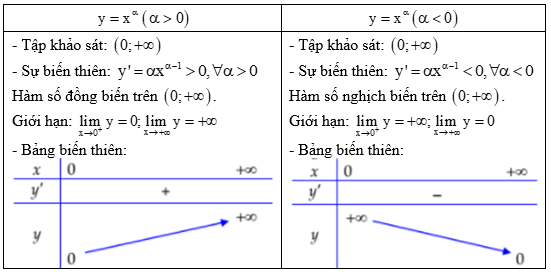
Đồ thị:
Luôn đi qua điểm (1;1)

- Trên đây ta chỉ xét chung các hàm số trên tập (0;+∞). Thực tế tập xác định của mỗi hàm số là khác nhau phụ thuộc vào điều kiện của α.
- Tránh nhầm lẫn tập (0;+∞) là tập xác định cho mọi hàm số lũy thừa.
II. Tìm tập xác định của hàm số
Phương pháp:
- Bước 1: Xác định số mũ α của hàm số.
- Bước 2: Nêu điều kiện để hàm số xác định.
+ α nguyên dương: D=R.
+ α nguyên âm hoặc α=0: D=R∖{0}.
+ α không nguyên: D=(0;+∞).
- Bước 3: Giải các bất phương trình ở trên để tìm tập xác định của hàm số.
III. Tính đạo hàm của hàm số
Phương pháp:
- Bước 1: Áp dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương để tính đạo hàm hàm số đã cho.
(u±v)′=u′±v′;(uv)′=u′v+uv′;(uv)′=u′v−uv′v2
- Bước 2: Tính đạo hàm các hàm số thành phần dựa vào công thức tính đạo hàm các hàm số cơ bản: hàm đa thức, phân thức, hàm mũ, logarit, lũy thừa,…
- Bước 3: Tính toán và kết luận.
IV. Tìm mỗi quan hệ của các số mũ của các hàm số lũy thừa khi biết đồ thị của chúng
Phương pháp:
Quan sát đồ thị hàm số và nhận xét tính đồng biến, nghịch biến và các điểm đi qua để suy ra tính chất của các số mũ.

