Đề bài
Cho hai dòng điện có cùng cường độ 8 A chạy trong hai dây dẫn thẳng dài, đặt vuông góc với nhau, cách nhau một khoảng 8,0 cm trong chân không : dây dẫn thứ nhất thẳng đứng có dòng điện chạy từ dưới lên trên, dây dẫn thứ hai thẳng ngang có dòng điện chạy từ trái qua phải. Xác định cảm ứng từ tại trung điểm của khoảng cách giữa hai dây dẫn này.
Phương pháp giải - Xem chi tiết
Sử dụng biểu thức tính cảm ứng từ: \(B= 2.10^{-7}\dfrac{I}{r}\)
Lời giải chi tiết
Khoảng cách giữa hai dây dẫn thẳng có dòng điện I1 và I2 là đoạn thẳng CD = d = 8,0 cm nằm trong cùng mặt phẳng ngang p chứa dòng điện I2.
Hai vectơ cảm ứng từ \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) lần lượt do I1 và I2 gây ra tại trung điểm M của đoạn CD có hướng như trên Hình IV. 1G:
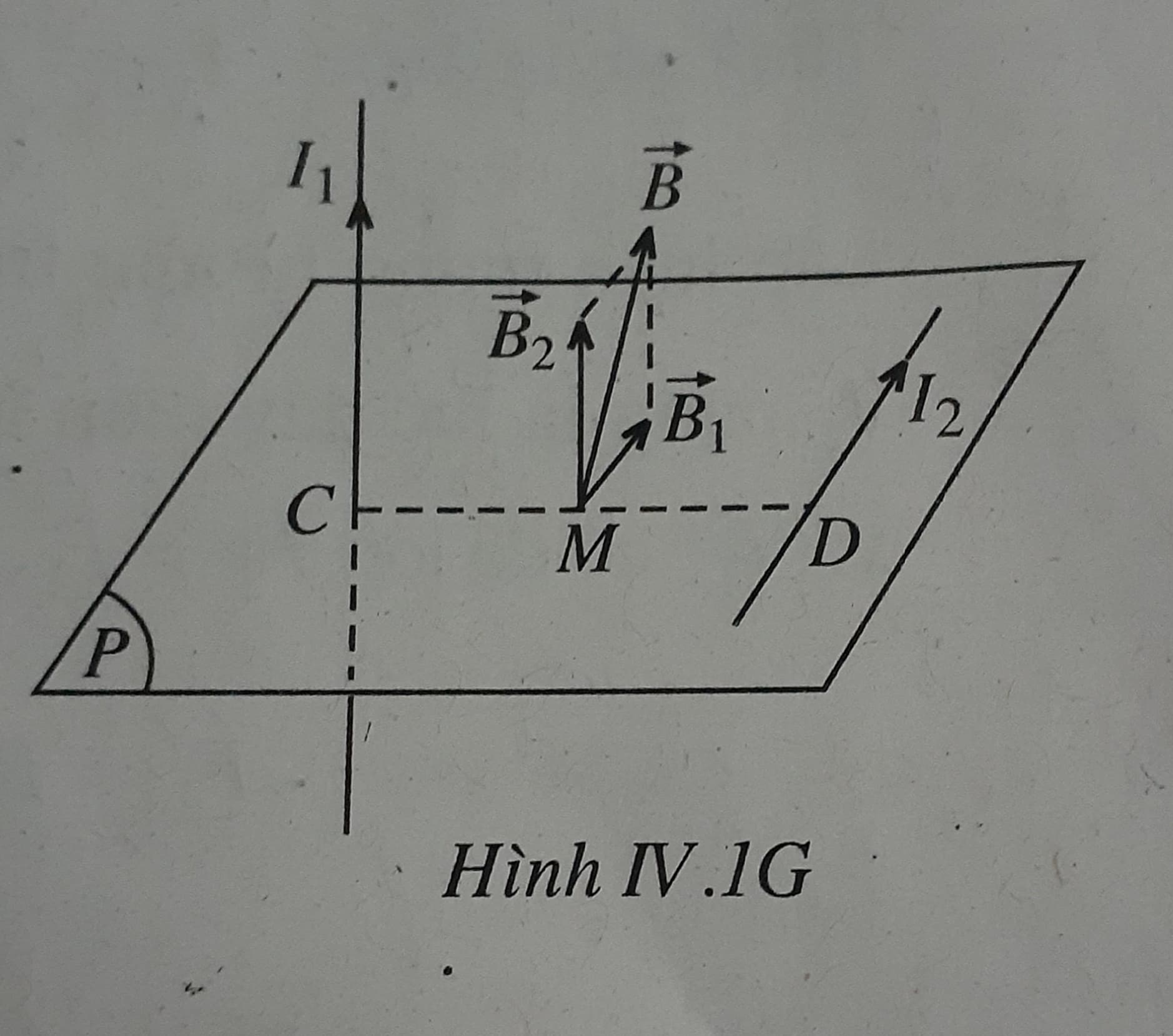
\(\overrightarrow {{B_1}} \) song song với dây dẫn có dòng điện I2 và cùng chiều với I2, \(\overrightarrow {{B_2}} \) song song với dây dẫn có dòng điện I1 và cùng chiều với I1, có độ lớn bằng nhau
\({B_1} = {B_2} = {2.10^{ - 7}}.{\dfrac{8,0}{4,0.10^{ - 2}}} = {4,0.10^{ - 5}}T\)
Vecto cảm ứng từ tổng hợp tại điểm M:
\(\overrightarrow {{B}} \)= \(\overrightarrow {{B_1}} \)+ \(\overrightarrow {{B_2}} \)
Vì \(\overrightarrow {{B_1}} \bot \overrightarrow {{B_2}} \) nên độ lớn của \(\overrightarrow {{B}} \) tính bằng:
\(B = {B_1}\sqrt 2 = 4\sqrt 2 {.10^{ - 5}}T\)

