Đề bài
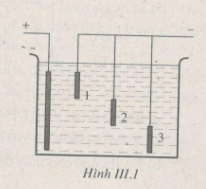
Trong bình điện phân dung dịch đồng sunphat (CuSO4) có anôt bằng đồng, người ta nối ba lá đồng mỏng 1, 2, 3 có cùng diện tích mặt ngoài 10 cm2 với catôt sao cho khoảng cách từ mỗi lá đồng đến anôt lần lượt là 10, 20, 30 cm (Hình III. l)
Đặt hiệu điện thế u = 15 V vào hai điện cực của bình điện phân. Đồng có khối lượng mol nguyên tử A = 63,5 g/mol và hoá trị n = 2. Điện trở suất của dung dịch điện phân là 0,20 Ω.m. Xác định :
a) Điện trở của mỗi phần dung dịch nằm giữa anôt và mỗi lá đồng 1,2, 3.
b) Khối lượng đồng bám vào mỗi lá đồng sau thời gian t = 1 giờ.
Phương pháp giải - Xem chi tiết
+ Sử dụng biểu thức tính điện trờ:\(R = \rho \dfrac{\ell}{S}\)
+ Sử dụng biểu thức thức Faraday về điện phân: \(m = \dfrac{1}{F}.\dfrac{A}{n}.It\)
Lời giải chi tiết
a) Bình điện phân chứa dung dịch muối của kim loại dùng làm các điện cực đóng vai trò như một điện trở thuần khi có dòng điện chạy qua nó. Do đó, điện trở và cường độ dòng điện chạy qua mỗi phần dung dịch điện phân giữa anot và mỗi lá đồng 1, 2, 3 được tính theo các công thức:
\(R = \rho \dfrac{\ell}{S};I = \dfrac{U}{R}\)
Vì các phần dung dịch này có cùng điện trở suất \(ρ = 0,20 Ω.m\) và cùng tiết diện \(S = 10.10^{-4}m^2\) nhưng có độ dài l khác nhau nên ta tìm được:
- Với l1= 10cm:
\({R_1} = 0,20.\dfrac{10.10^{ - 2}}{10.10^{ - 4}} = 20\Omega\)
\({I_1} = \dfrac{U}{R_1} = \dfrac{15}{20} = 0,75A\)
- Với l2 = 20cm:
\({R_2} = 0,20.\dfrac{20.10^{ - 2}}{10.10^{ - 4}} = 40\Omega\)
\({I_1} =\dfrac {U}{R_1}= \dfrac{15}{40} = 0,375A\)
- Với l3 = 30cm:
\({R_3} = 0,20.\dfrac{30.10^{ - 2}}{10.10^{ - 4}} = 60\Omega\)
\({I_1} = \dfrac{U}{R_1} = \dfrac{15}{60} = 0,25A\)
b) Theo công thức Faraday về điện phân, đồng bám vào mỗi lá đồng 1,2,3 sau thời gian \(t = 1h = 3600s\) có khối lượng tương ứng tính bằng:
\(m = \dfrac{1}{F}.\dfrac{A}{n}.It = \dfrac{1}{96500}.\dfrac{A}{n}.It\)
- Với I1= 0,75A:
\({m_1} = \dfrac{1}{96500}.\dfrac{63,5}{2}.0,75.3600 \\\approx 888mg\)
- Với I2= 0,375A:
\({m_1} = \dfrac{1}{96500}.\dfrac{63,5}{2}.0,375.3600 \\\approx 444mg\)
- Với I3= 0,25A:
\({m_1} =\dfrac {1}{96500}.\dfrac{63,5}{2}.0,25.3600 \\\approx 296mg\)