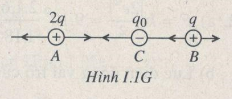
Đề bài
Có một hệ ba điện tích điểm: q1 = 2q, đặt tại điểm A; q2 = q đặt tại điểm B, với q dương; và q3 = q0 đặt tại điểm C, với q0 âm. Bỏ qua trọng lượng của ba điện tích. Hệ ba điện tích này nằm cân bằng trong chân không.
a) Các điện tích này phải sắp xếp như thế nào?
b) Biết AB = a. Tính BC theo a.
c) Tính q theo q0.
Phương pháp giải - Xem chi tiết
Sử dụng biểu thức tính lực điện : \( F= k{\dfrac{qQ}{r^2}}\)
Lời giải chi tiết
a) Mỗi điện tích chịu tác dụng của hai lực. Muốn hai lực này cân bằng nhau thì chúng phải có cùng phương, ngược chiều và cùng cường độ. Như vậy, ba điểm A, B, C phải nằm trên cùng một đường thẳng.
Điện tích âm q0 phải nằm xen giữa hai điện tích dương và phải nằm gần điện tích có độ lớn q (Hình I.1. G)
b) Đặt BC = x và AB = a. Ta có AC = x – a.
Cường độ của lực mà điện tích q tác dụng lên q0 là :
\({F_{BC}} = k{\dfrac{qq_0}{x^2}}\)
Cường độ của lực mà điện tích 2q tác dụng lên q0 là :
\({F_{AC}} = k{\dfrac{2qq_0}{(a - x)^2}}\)
Với FBC = FAC thì ta có:
\(\dfrac{1}{x^2} = \dfrac{2}{(a - x)^2}\)
Giải ra ta được \(x = a(\sqrt 2 - 1)\). Vậy \(BC = a(\sqrt 2 - 1) \approx 0,414a\)
c) Xét sự cân bằng của điện tích q.
Cường độ của lực mà điện tích 2q tác dụng lên q là :
\({F_{AB}} = k{\dfrac{2q^2}{a^2}}\)
Cường độ của lực mà điện tích q0 tác dụng lên q là :
\({F_{CB}} = k{\dfrac{q_0q}{x^2}}\)
Vì FAB = FCB nên ta có:
\(\dfrac{2|q|}{a^2} = \dfrac{|q_0|}{x^2}\)
\(\eqalign{
& \left| q \right| = {\dfrac{a^2}{2x^2}}\left| {{q_0}} \right| = {1 \over {2{{\left( {\sqrt 2 - 1} \right)}^2}}}\left| {{q_0}} \right| \approx 2,91\left| {{q_0}} \right| \cr
& q \approx - 2,91{q_0} \cr} \)