Đề bài
Một người có khoảng cực cận OCc = 15 cm và khoảng nhìn rõ (khoảng cách từ điểm cực cận đến điểm cực viễn) là 35 cm.
Người này quan sát một vật nhỏ qua kính lúp có tiêu cự 5 cm. Mắt đặt cách kính 10 cm.
Năng suất phân li của mắt người này là 1’. Tính khoảng cách ngắn nhất giữa hai điểm trên vật mà mắt người này còn phân biệt được khi ngắm chừng ở điểm cực cận.
Phương pháp giải - Xem chi tiết
Vận dụng kiến thức về kính bội giác.
Lời giải chi tiết
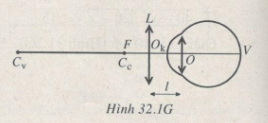
Hình 32.1G.
Quan sát vật qua kính nghĩa là quan sát ảnh của vật tạo bởi kính.
Phải có α ≥ αmin.
Ngắm chừng ở điểm cực cận: A’ ≡ CC
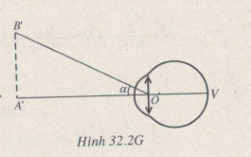
Ta có: \(α ≈ tanα =\dfrac{A'B'}{OC_c}\) (Hình 32.2G)
Vậy
\(\dfrac{{A'B'}}{{O{C_C}}} \geqslant {\alpha _{\min }} \Rightarrow A'B' \geqslant O{C_C}.{\alpha _{\min }}\)
Khoảng cách ngắn nhất trên vật còn phân biệt được:
\(\begin{gathered}
{k_C}.AB \geqslant O{C_C}.{\alpha _{\min }} \hfill \\
\Rightarrow A{B_{\min }} = \dfrac{{O{C_C}}}{{{k_C}}}.{\alpha _{\min }} = \dfrac{{15}}{2}.\dfrac{1}{{3500}} \approx 21,4\mu m \hfill \\
\end{gathered} \)