Đề bài
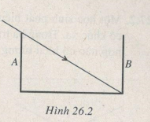
Một cái máng nước sâu 30 cm, rộng 40 cm có hai thành bên thẳng đứng. Đúng lúc máng cạn nước thì có bóng râm của thành A kéo dài tới đúng chân thành B đối diện (Hình 26.2). Người ta đổ nước vào máng đến một độ cao h thì bóng của thành A ngắn bớt đi 7 cm so với trước. Biết chiết suất của nước là n = 4/3. Hãy tính h và vẽ tia sáng giới hạn bóng râm của thành máng khi có nước.
Phương pháp giải - Xem chi tiết
Vận dụng kiến thức về định luật khúc xạ ánh sáng.
Lời giải chi tiết
CC’ = 7cm
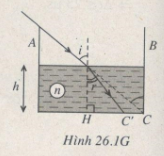
\(=>HC – HC’ = h(tani – tanr) = 7cm\) (Hình 26.1G).
\(\eqalign{
& \tan i = {4 \over 3};{\mathop{\rm t}\nolimits} {\rm{anr}} = {{{\mathop{\rm s}\nolimits} {\rm{inr}}} \over {{\rm{cosr}}}};{\mathop{\rm s}\nolimits} {\rm{inr}} = {{\sin i} \over n} = {3 \over 5} \cr
& {\rm{cosr = }}\sqrt {1 - {{\sin }^2}r} = {4 \over 5};{\mathop{\rm t}\nolimits} {\rm{anr}} = {3 \over 4} \cr} \)
Do đó:
\(h\left( {\dfrac{4}{3} - \dfrac{3}{4}} \right) = 7cm \Rightarrow h = 12cm\)