Đề bài
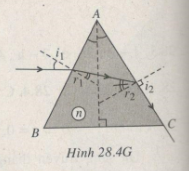
Một lăng kính có tiết diện vuông góc là một tam giác đều ABC. Một chùm tia sáng đơn sắc hẹp SI được chiếu tới mặt AB trong mặt phẳng của tiết diện vuông góc và theo phương vuông góc với đường cao AH của ABC. Chùm tia ló khỏi mặt AC theo phương sát với mặt này. Tính chiết suất của lăng kính.
Phương pháp giải - Xem chi tiết
Sử dụng công thức lăng kính: \(sini=nsinr\) ; \(A=r_1+r_2\)
Lời giải chi tiết
Theo đề bài: i = 300; \(sinr_1 = \dfrac{1}{2n}\)
i2 = 900 (HÌnh 28.4G); r2 = igh --> \(sinr_2 = \dfrac{1}{n}\)
Nhưng r1 = A – r2 – 600 - igh
\(\begin{array}{l}
\Rightarrow \dfrac{1}{{2n}} = \frac{{\sqrt 3 }}{2}.\dfrac{{\sqrt {{n^2} - 1} }}{n} - \dfrac{1}{n}.\dfrac{1}{2}\\
\Rightarrow n = \sqrt {1 + \dfrac{4}{3}} = \sqrt {\frac{7}{3}} \approx 1,53
\end{array}\)