Đề bài
Cho một nguồn điện có suất điện động E=24V và điện trở trong có \(r=6\Omega\)
a) Có thể mắc nhiều nhất bao nhiêu bóng đèn loại 6V-3W vào nguồn điện đã cho trên đây để các đèn sáng bình thường? Vẽ sơ đồ cách mắc.
b) Nếu chỉ có 6 bóng đèn loại trên đây thì phải mắc chúng vào nguồn điện đã cho theo sơ đồ nào để các đèn sáng bình thường. Trong các cách mắc này thì cách nào lợi hơn? vì sao?
Phương pháp giải - Xem chi tiết
+ Sử dụng định luật Ôm cho mạch kín: \(I=\dfrac{E}{R+r}\)
+ Sử dụng biểu thức tính cường độ qua đèn: \(I_0=\dfrac{P_đ}{U_đ}\)
Lời giải chi tiết
Cường độ qua đèn khi sáng bình thường:
\(I_0=\dfrac{P_đ}{U_đ}\)
Điện trở của đèn là:
\(R_0=\dfrac{U_d^2}{P_d}=12\Omega\)
Gỉa sử các đèn mắc thành y dãy song song, mỗi dãy có x đèn.
Cường độ dòng điện qua mạch chính là: \(I= y.I_0\)
Theo định luật Ôm cho mạch kín: \(I=\dfrac{E}{R+r}\)
\(y.I_0=\dfrac{E}{\dfrac{xR_0}{y}+r}\)
Suy ra:
\(xR_0I_0+yI_0r=E\)
\(6x+3y=24\)
\(2x+y=8\) (1)
a) Ta có: \( 2x+y=8\)
Số đèn: \(N=xy\)
\(=> 2x^2 - 8x + N=0\)
\( \Delta' = 16 - 2N\)
Điều kiện để phương trình có nghiệm : \( \Delta' = 16 - 2N > 0\)
Hay \( N<8\)
Vậy số đèn tối đa có thể thắp sáng bình thường là : N=8
Khi đó: \( \Delta' = 0 => x = 2, y=4\)
=> Các đèn phải mắc thành 4 dãy, mỗi dãy 2 đèn.
Mạch điện có sơ đồ như hình dưới đây:
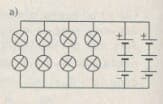
b) Có 6 đèn:
Số đèn là: \(N=xy= 6\)
Từ (1) => \( 2x+\dfrac{6}{x}=8\)
Hay \(x^2-4x+3=0\)
Nghiệm của pt: \(x_1=1\) hoặc \(x_2=3\)
Vậy có hai cách mắc để đèn sáng bình thường.
- Mắc thành 6 dãy song song mỗi dãy 1 đèn
Hiệu suất: \(H= \dfrac{U}{E} = \dfrac{x_1U_đ}{E} = \dfrac{1.6}{24}=0,25=25\%\)
- Mắc thành 2 dãy song song mỗi dãy 3 đèn nối tiếp.
Hiệu suất: \(H= \dfrac{U}{E} = \dfrac{x_2U_đ}{E} = \dfrac{3.6}{24}=0,75=75\%\)
Vậy mắc theo cách thứ hai có lợi hơn.

