Đề bài
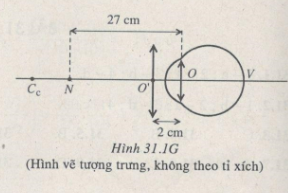
Một người đứng tuổi nhìn rõ được các vật ở xa. Muốn nhìn rõ vật gần
nhất cách mắt 27 cm thì phải đeo kính + 2,5 dp cách mắt 2 cm.
a) Xác định các điểm Cc và Cv của mắt.
b) Nếu đeo kính sát mắt thì có thể nhìn rõ các vật ở trong khoảng nào ?
Phương pháp giải - Xem chi tiết
+ Sử dụng biểu thức tính: \(f_k=\dfrac{1}{d_k}\)
+ Tiêu cự của hệ thấu kính: \(\dfrac{1}{f} = \dfrac{1}{{{f_{max}}}} + \dfrac{1}{{{f_k}}}\)
Lời giải chi tiết
a) Vì CV--> ∞ \( \Rightarrow {f_k} = \dfrac{1}{{{D_k}}} = \dfrac{1}{{2,5}} = 0,4m = 40cm\)
Ta có:
\(\begin{array}{l}
\dfrac{1}{{O'N}} - \dfrac{1}{{O'{C_C}}} = \dfrac{1}{{{f_k}}} \Rightarrow \dfrac{1}{{O'{C_C}}} = \dfrac{1}{{25}} - \dfrac{1}{{40}}\\
\Rightarrow O'{C_C} = \dfrac{{25.40}}{{40 - 25}} = \dfrac{{200}}{3}cm
\end{array}\)
Vậy
\(O{C_C} = \dfrac{{200}}{3} + 2 = \dfrac{{206}}{3} \approx 68,6cm\)
b) Tiêu cự của thấu kính tương đương với hệ (mắt + kính):
\(\dfrac{1}{f} = \dfrac{1}{{{f_{mat}}}} + \dfrac{1}{{{f_k}}}\)
Khoảng phải tìm giới hạn bởi M và N xác định như sau:
| \(M\xrightarrow{{(mat + kinh)}}M' \equiv V\) * Có kính: \(\dfrac{1}{{OM}} + \dfrac{1}{{OV}} = \dfrac{1}{{{f_{max}}}} + \dfrac{1}{{{f_k}}}\) * Không kính: \(\begin{gathered}
| \(N\xrightarrow{{(mat + kinh)}}N' \equiv V\) * Có kính: \(\dfrac{1}{{ON}} + \dfrac{1}{{OV}} = \dfrac{1}{{{f_{\min }}}} + \dfrac{1}{{{f_k}}}\) * Không kính: \(\begin{gathered} |