Đường tròn trong mặt phẳng tọa độ

$(C):{x^2} + {y^2} - 4x - 2y = 0$ có tâm $I(2;1)$ và bán kính $R = \sqrt {{2^2} + {1^2}}  = \sqrt 5$

Ta có $IH = d\left( {I,d} \right) = \dfrac{{|2 - 1 + 1|}}{{\sqrt 2 }} = \sqrt 2  < R$. Suy ra $IH < R \Leftrightarrow d$ cắt $\left( C \right)$ tại hai điểm phân biệt.

$(C):{x^2} + {y^2} - 2x + 4y - 4 = 0$ có tâm $I\left( {1; - 2} \right)$ và bán kính $R = \sqrt {{1^2} + {{\left( { - 2} \right)}^2} + 4}  = 3$

Nếu d có phương trình $x = 1$ ta có $d\left( {I;d} \right) = \left| {1 - 1} \right| = 0 \ne R$. Loại A

Nếu d có phương trình $x + y - 2 = 0$ thì ta có $d\left( {I;d} \right) = \dfrac{{\left| {1 - 2 - 2} \right|}}{{\sqrt 2 }} = \dfrac{3}{{\sqrt 2 }} \ne R$. Loại B

Nếu d có phương trình $2x + y - 1 = 0$ thì ta có $d\left( {I;d} \right) = \dfrac{{\left| {2.1 - 2 - 1} \right|}}{{\sqrt 5 }} = \dfrac{1}{{\sqrt 5 }} \ne R$. Loại C

Nếu d có phương trình $y = 1$ ta có $d\left( {I;R} \right) = \left| {1 - \left( { - 2} \right)} \right| = 3 = R$.

Vậy $d$ là tiếp tuyến của $(C )$

$(C):{x^2} + {y^2} + 4x - 2y - 20 = 0,$ có tâm $I\left( { - 2;1} \right);\,\,R = \sqrt {{{\left( { - 2} \right)}^2} + {1^2} + 20}  = 5$

Tiếp tuyến vuông góc với đường thẳng $(d):3x + 4y - 37 = 0$ nên phương trình tiếp tuyến có dạng $4x - 3y + c = 0$ (d’)

Vì d’ là tiếp tuyến của đường tròn có tâm $I\left( { - 2;1} \right)$ và $R = 5$ nên ta có

$d\left( {I;d'} \right) = R \Leftrightarrow \dfrac{{\left| {4.\left( { - 2} \right) - 3.1 + c} \right|}}{5} = 5$$\Leftrightarrow |c - 11| = 25$$\Leftrightarrow c = 36$  hoặc $c =  - 14$

Đường tròn $\left( C \right)$  có tâm $I\left( {1;3} \right)$   và bán kính $R = 2.$

Gọi $d$  là tiếp tuyến cần tìm.

Ta có $d$  đi qua điểm $M\left( {4;1} \right)$  nên phương trình $d$  có 2 dạng.

+) ${d_1}:x = 4$. Khi đó $d\left( {I;d} \right) = \left| {4 - 1} \right| = 3 > R$ nên ${d_1}:x = 4$ không phải là tiếp tuyến.

+) ${d_2}:y = k\left( {x - 4} \right) + 1 \Leftrightarrow kx - y + 1 - 4k = 0$

Vì ${d_2}$  là tiếp tuyến nên ta có

 $d\left( {I;{d_2}} \right) = R \Leftrightarrow \dfrac{{\left| {k - 3 + 1 - 4k} \right|}}{{\sqrt {{k^2} + {1^2}} }} = 2$$\Leftrightarrow 5{k^{^2}} + 12k = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{k = 0}\\{k = \dfrac{{ - 12}}{5}}\end{array}} \right.$

Vậy có 2 tiếp tuyến thỏa yêu cầu đề bài $y = 1$ và $12x + 5y - 53 = 0$

Viết lại phương trình của $\left( C \right)$  dưới dạng: ${\left( {x-3} \right)^2} + {y^2} = 4.$

Từ đó, $\left( C \right)$  có tâm $I\left( {3;0} \right)$  và bán kính $R = 2$

Giao của đường tròn với trục tung $\left( {x = 0} \right)$  là: ${\left( { - 3} \right)^2} + {y^2} = 4.$

Nên ${y^2} =  - 5$  (vô lý)

Suy ra trục tung không có điểm chung với đường tròn $\left( C \right).$

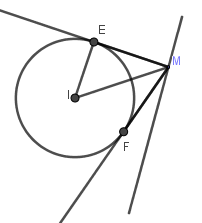
Gọi $M\left( {0;m} \right) \in Oy$ mà góc giữa hai tiếp tuyến $ME,MF$ bằng ${60^0}$

Khi đó $\widehat {IME} = {30^0}$ suy ra $MI = \dfrac{{IE}}{{\sin \widehat {IME}}} = \dfrac{2}{{\sin {{30}^0}}} = 4$

Do đó $\sqrt {{{\left( {3 - 0} \right)}^2} + {{\left( {0 - m} \right)}^2}}  = 4$ $\Leftrightarrow \sqrt {9 + {m^2}}  = 4 \Leftrightarrow m =  \pm \sqrt 7$

Vậy có hai điểm $M$ cần tìm là $\left( {0;\sqrt 7 } \right)$ và $\left( {0; - \sqrt 7 } \right)$

Tâm $I$ của đường tròn nằm trên đường trung trực $d$ của đoạn $AB$.

Gọi d là đường trung trực của AB thì d đi qua trung điểm $M\left( {1;2} \right)$ của AB và có VTPT là $\overrightarrow {AB}  = (4;2)$

$\begin{array}{l} \Rightarrow d:4\left( {x - 1} \right) + 2\left( {y - 2} \right) = 0\\ \Leftrightarrow 4x - 4 + 2y - 4 = 0\\ \Leftrightarrow 4x + 2y - 8 = 0\\ \Leftrightarrow 2x + y - 4 = 0 \end{array}$

$\Rightarrow$tâm $I\left( {a;4-2a} \right)$

Ta có $IA = d\left( {I,\Delta } \right)$ $\Leftrightarrow \left| {11a - 8} \right| = 5\sqrt {5{a^2} - 10a + 10}$  $\Leftrightarrow 2{a^2}-37a + 93 = 0$ $\Leftrightarrow \left[ \begin{array}{l}a = 3\\a = \dfrac{{31}}{2}\end{array} \right.$

- Với $a = 3 \Rightarrow I\left( {3;-2} \right),R = 5$ $\Rightarrow \left( C \right):{\left( {x-3} \right)^2} + {\left( {y + 2} \right)^2} = 25$

- Với $a = \dfrac{{31}}{2}$ $\Rightarrow I\left( {\dfrac{{31}}{2}; - 27} \right)$, $R = \dfrac{{65}}{2}$ $\Rightarrow \left( C \right):{\left( {x - \dfrac{{31}}{2}} \right)^2} + {(y + 27)^2} = \dfrac{{4225}}{4}$

$(C)$ có tâm $I(1;-2)$ và bán kính $R = 3.$

Ta có: $\Delta PAB$  đều

$\begin{array}{l} \Rightarrow \widehat {APB} = {60^0} \Rightarrow \widehat {API} = \frac{1}{2}\widehat {APB} = {30^0}\\ \Rightarrow IP = \frac{{IA}}{{\sin \widehat {API}}} = \frac{3}{{\sin {{30}^0}}} = 6 \end{array}$

Suy ra $P$ thuộc đường tròn $(C')$ tâm $I,$ bán kính $R ' = 6.$

Trên $d$ có duy nhất một điểm $P$ thỏa mãn yêu cầu bài toán khi và chỉ khi $d$ tiếp xúc với $(C')$ tại $P$

$\Leftrightarrow d\left( {I,d} \right) = R'$

$\begin{array}{l} \Leftrightarrow \frac{{\left| {3.1 - 4.\left( { - 2} \right) + m} \right|}}{{\sqrt {{3^2} + {{\left( { - 4} \right)}^2}} }} = 6 \Leftrightarrow \frac{{\left| {m + 11} \right|}}{5} = 6\\ \Leftrightarrow \left| {m + 11} \right| = 30 \Leftrightarrow \left[ \begin{array}{l} m + 11 = 30\\ m + 11 = - 30 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} m = 19\\ m = - 41 \end{array} \right. \end{array}$

Vì $\Delta$ song song với $d$ nên phương trình $\Delta$ có dạng $x - y + m = 0$

Kẻ $IH$ vuông góc vơi $MN$ ta có $HM = HN = \dfrac{1}{2}MN = 1$

Đường tròn $(C )$ có tâm $I(-1;2)$ và bán kính $R = \sqrt 5$

Từ đó $IH = \sqrt {I{M^2} - H{M^2}}  = 2 \Leftrightarrow d\left( {I;\Delta } \right) = 2 \Leftrightarrow \dfrac{{\left| { - 1 - 2 + m} \right|}}{{\sqrt {{1^2} + {1^2}} }} = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2\sqrt 2  + 3}\\{m =  - 2\sqrt 2  + 3}\end{array}} \right.$

Vậy có $2$ tiếp tuyến cần tìm $x - y + 2\sqrt 2  + 3 = 0$ và $x - y - 2\sqrt 2  + 3 = 0$

$d:x + 2y - 4 = 0$.

Đường tròn $\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 5$ có tâm $I\left( {2;1} \right)$ và bán kính $R = \sqrt 5 .$

Ta có: $d\left( {I;\,\,d} \right) = \dfrac{{\left| {2 + 2.1 - 4} \right|}}{{\sqrt {1 + {2^2}} }} = 0 \Rightarrow I \in d.$

$\Rightarrow d$ là đường thẳng đi qua đường kính của đường tròn $\left( C \right)$

$\Rightarrow d$ cắt $\left( C \right)$ theo dây cung $AB = 2R = 2\sqrt 5 .$

$\left( C \right):{x^2} + {y^2} + 2x + 4y - 31 = 0$$\Leftrightarrow \left( C \right):{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 36.$

Vậy $I\left( { - 1; - 2} \right),R = 6.$

Gọi $H$ là chân đường cao hạ từ $I$ xuống $AB$, thì $H$ là trung điểm của $AB$.

${S_{IAB}} = \dfrac{1}{2}IH.AB = IH.HA\mathop  \le \limits^{AM - GM} \dfrac{{I{H^2} + H{A^2}}}{2} = \dfrac{{I{A^2}}}{2} = \dfrac{{{R^2}}}{2} = 18.$

Vậy diện tích tam giác $IAB$ có giá trị lớn nhất là $18.$

Phương trình đường tròn $\left( C \right)$  tâm $I\left( {a;b} \right)$, bán kính $R$ là :${(x - a)^2} + {(y - b)^2} = {R^2}$

Phương trình ${x^2} + {y^2} + 2ax + 2by + c = 0{\rm{ }}$ với điều kiện ${a^2} + {b^2} - c > 0$, là phương trình đường tròn tâm $I\left( { - a; - b} \right)$ bán kính $R = \sqrt {{a^2} + {b^2} - c}$

Do đó đáp án A sai.

${x^2} + {y^2} + 2ax + 2by + c = 0,$ là phương trình đường tròn khi ${R^2} = {a^2} + {b^2} - c$. Điều này có nghĩa là ${a^2} + {b^2} - c > 0$  hay ${a^2} + {b^2} > c$.

${x^2} + {y^2} - 2\left( {m + 2} \right)x + 4my + 19m - 6 = 0\,\,\,\,\left( * \right)$

(*) là phương trình đường tròn khi ${\left( {m + 2} \right)^2} + {\left( {2m} \right)^2} - 19m + 6 > 0 \Leftrightarrow 5{m^2} - 15m + 10 > 0$$\Leftrightarrow$ $m < 1$ hoặc $m > 2$

Đáp án A: ${x^2} + 2{y^2} - 4x - 8y + 1 = 0$ không phải là phương trình đường tròn vì hệ số của $x^2$ là 1 và của $y^2$ là 2.

Đáp án B: $4{x^2} + {y^2} - 10x - 6y - 2 = 0$ không phải là phương trình đường tròn vì hệ số của $x^2$ là 4 và của $y^2$ là 1.

Đáp án C: ${x^2} + {y^2} - 2x - 8y + 20 = 0$ có $a = 1\,\,,b = 4,\,\,c = 20$.

Ta thấy ${a^2} + {b^2} =1^2+4^2=17 < 20 = c$. Đây không phải là một phương trình đường tròn.

Đáp án D: ${x^2} + {y^2} - 4x + 6y - 12 = 0$ có $a = 2,\,\,b =  - 3,\,\,c =  - 12$.

Ta thấy ${a^2} + {b^2} =2^2+(-3)^2=13 > -12 = c$. Đây là một phương trình đường tròn.

${x^2} + {y^2} - 2x + 4y + 1 = 0$ có hệ số $a = 1,b =  - 2,c = 1$  sẽ có tâm $I\left( {1; - 2} \right)$ và $R = \sqrt {{{\left( { - 1} \right)}^2} + {2^2} - 1}  = 2$

$(C):{x^2} + {y^2} + 2x + 4y - 20 = 0$ có $a =  - 1,\,\,b =  - 2,c =  - 20$ sẽ có tâm $I\left( { - 1; - 2} \right)$ và bán kính $R = \sqrt {{1^2} + {2^2} + 20}  = 5$. 

Thay tọa độ các điểm ở đáp án C và D vào phương trình đường tròn ta thấy hai đáp án đều đúng.

Suy ra mệnh đề sai là mệnh đề ở đáp án A.

Gọi đường tròn có phương trình ${x^2} + {y^2} + 2ax + 2by + c = 0\,\left( C \right)$

$A,\,B,\,C \in \left( C \right)$ $\Leftrightarrow \left\{ \begin{array}{l}16 + 8b + c = 0\\20 + 4a + 8b + c = 0\\16 + 8a + c = 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}a =  - 1\\b =  - 1\\c =  - 8\end{array} \right. \to I\left( {1;1} \right)$

${x^2} + {y^2} = 1.$ Thay $x = 0,y = 0$ ta có ${0^2} + {0^2} = 1$ là mệnh đề A sai.

${x^2} + {y^2} - x - y + 2 = 0$. Thay $x = 0,y = 0$ ta có $2 = 0$ là mệnh đề B sai.

${x^2} + {y^2} - 4x - 4y + 8 = 0.$ Thay $x = 0,y = 0$ ta có $8 = 0$ là mệnh đề C sai.

${\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 25.$ Thay $x = 0,y = 0$ ta có ${\left( { - 3} \right)^2} + {\left( { - 4} \right)^2} = 25$ là mệnh đề đúng. Vậy ${\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 25.$ đi qua gốc tọa độ.

Ta có: $R = IA = \sqrt {{{\left( {1 - 2} \right)}^2} + {{\left( {3 + 4} \right)}^2}}  = \sqrt {50}$

Phương trình đường tròn $(C)$ có tâm $I\left( {2; - 4} \right)$  có bán kính $R = \sqrt {50}$ là: ${\left( {x - 2} \right)^2} + {\left( {y + 4} \right)^2} = 50.$