Trong mặt phẳng với hệ tọa độ $Oxy,$ cho đường tròn $\left( C \right)$ có phương trình: ${x^2} + {y^2}-6x + 5 = 0.$ Tìm điểm $M$ thuộc trục tung sao cho qua $M$ kẻ được hai tiếp tuyến với $\left( C \right)$ mà góc giữa hai tiếp tuyến đó bằng ${60^0}.$
Trả lời bởi giáo viên
Viết lại phương trình của $\left( C \right)$ dưới dạng: ${\left( {x-3} \right)^2} + {y^2} = 4.$
Từ đó, $\left( C \right)$ có tâm $I\left( {3;0} \right)$ và bán kính $R = 2$
Giao của đường tròn với trục tung $\left( {x = 0} \right)$ là: ${\left( { - 3} \right)^2} + {y^2} = 4.$
Nên ${y^2} = - 5$ (vô lý)
Suy ra trục tung không có điểm chung với đường tròn $\left( C \right).$
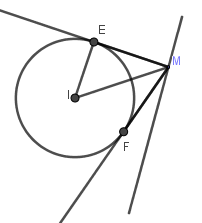
Gọi \(M\left( {0;m} \right) \in Oy\) mà góc giữa hai tiếp tuyến \(ME,MF\) bằng \({60^0}\)
Khi đó \(\widehat {IME} = {30^0}\) suy ra \(MI = \dfrac{{IE}}{{\sin \widehat {IME}}} = \dfrac{2}{{\sin {{30}^0}}} = 4\)
Do đó \(\sqrt {{{\left( {3 - 0} \right)}^2} + {{\left( {0 - m} \right)}^2}} = 4\) \( \Leftrightarrow \sqrt {9 + {m^2}} = 4 \Leftrightarrow m = \pm \sqrt 7 \)
Vậy có hai điểm \(M\) cần tìm là \(\left( {0;\sqrt 7 } \right)\) và \(\left( {0; - \sqrt 7 } \right)\)
Hướng dẫn giải:
Gọi tọa độ $M(0;m)$, vẽ hình và sử dụng điều kiện góc giữa hai tiếp tuyến bằng $60^0$ để tìm $M$

