Các dạng toán về phép nhân, phép chia các số nguyên (tiếp)

Ta có: \( - 8 =  - 1.8 = 1.\left( { - 8} \right) =  - 2.4 = 2.\left( { - 4} \right)\)

Tập hợp các ước của \( - 8\) là: \(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)

Vì trong tích có một thừa số bằng \(0\) nên \(M = 0\)

$a + 4$ là ước của $9$
$ \Rightarrow \;\left( {a + 4} \right) \in U\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\;$ 
Ta có bảng giá trị như sau:

Vậy giá trị lớn nhất của \(a\) là \(a = 5\)

Ta có:

\(\left( { - 154 + x} \right) \, \vdots \, 3\)

\(\left( { - 153 - 1 + x} \right) \, \vdots \, 3\)

Suy ra \(\left( {x - 1} \right) \, \vdots \, 3\) (do \( - 153 \, \vdots \, 3\))

Do đó \(x - 1 = 3k \Rightarrow x = 3k + 1\)

Vậy \(x\) chia cho \(3\) dư \(1.\)

$\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$$ \Rightarrow \left( {n + 1} \right) + 4 \, \vdots \,  \left( {n{\rm{ }} + 1} \right)$

Vì \(n + 1 \, \vdots \, n + 1\) và \(n \in Z\) nên để \(n + 5 \, \vdots \, n + 1\) thì \(4 \, \vdots \, n + 1\)

Hay \(n + 1 \in U\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\)

Ta có bảng:

Vậy \(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)

Vì \(10\) là bội của \(2a + 5\) nên \(2a + 5\) là ước của \(10\)

\(U\left( {10} \right) = \left\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}\)

Ta có bảng:

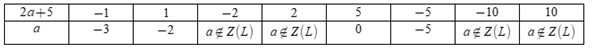
Mà \(a < 5\) nên \(a \in \left\{ { - 3; - 2;0; - 5} \right\}\)

Vậy có \(4\) giá trị nguyên của \(a\) thỏa mãn bài toán.

Ta có:

\(\begin{array}{l}a \, \vdots \, b \Rightarrow a = b.{q_1}\left( {{q_1} \in Z} \right)\\b \, \vdots \, a \Rightarrow b = a.{q_2}\left( {{q_2} \in Z} \right)\end{array}\)

Suy ra \(a = b.{q_1} = \left( {a.{q_2}} \right).{q_1} = a.\left( {{q_1}{q_2}} \right)\)

Vì \(a \ne 0\) nên \(a = a\left( {{q_1}{q_2}} \right) \Rightarrow 1 = {q_1}{q_2}\)

Mà \({q_1},{q_2} \in Z\) nên \({q_1} = {q_2} = 1\) hoặc \({q_1} = {q_2} =  - 1\)

Do đó \(a = b\) hoặc \(a =  - b\)

Ta có:\({n^2} - 7 = {n^2} + 3n - 3n - 9 + 2\)\( = n\left( {n + 3} \right) - 3\left( {n + 3} \right) + 2\)\( = \left( {n - 3} \right)\left( {n + 3} \right) + 2\)

Vì \(n \in Z\) nên để \({n^2} - 7\) là bội của \(n + 3\) thì \(2\) là bội của \(n + 3\) hay \(n + 3\) là ước của \(2\)

\(Ư\left( 2 \right) = \left\{ { \pm 1; \pm 2} \right\}\) nên \(n + 3 \in \left\{ { \pm 1; \pm 2} \right\}\)

Ta có bảng:

Vậy \(n \in A = \left\{ { - 5; - 4; - 2; - 1} \right\}\)

Do đó tổng các phần tử của \(A\) là \(\left( { - 5} \right) + \left( { - 4} \right) + \left( { - 2} \right) + \left( { - 1} \right) =  - 12\)

Ta có:

\(\begin{array}{l}5x + 46y = 5x + 30y + 16y\\ = \left( {5x + 30y} \right) + 16y\\ = 5\left( {x + 6y} \right) + 16y\end{array}\)

Vì \(5x + 46y\) chia hết cho $16$  và $16y$ chia hết cho $16$ nên suy ra \(5\left( {x + 6y} \right)\) chia hết cho $16.$

Mà $5$  không chia hết cho $16$ nên suy ra \(x + 6y\) chia hết cho $16$

Vậy nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) cũng chia hết cho $16.$

Vì \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(n - 1\),

Nên \(n - 1\) khác \(0\) và \(n + 5\) khác \(0\)

Nên \(n + 5,n - 1\) là hai số đối nhau

Do đó:

\((n + 5) + (n - 1) = 0\)

\(2n + 5 - 1 = 0\)

\(2n + 4 = 0\)

\(2n = -4\)

\(n=-2\)

Vậy có 1 số nguyên n thỏa mãn bài toán.

$A = ax - ay + bx - by$ $ = (ax - ay) + (bx - by)$ $ = a.(x - y) + b.(x - y)$ $ = (a + b).(x - y)$

Thay $a + b =  - 5;x - y =  - 2$ ta được:

\(A = \left( { - 5} \right).\left( { - 2} \right) = 10\)

\(\begin{array}{l}\left( {x + 1} \right) + \left( {x + 2} \right) + ... + \left( {x + 99} \right) + \left( {x + 100} \right) = 0\\(x + x + .... + x) + (1 + 2 + ... + 100) = 0\\100{\rm{x}} + (100 + 1).100:2 = 0\\100{\rm{x}} + 5050 = 0\\100{\rm{x}} =  - 5050\\x =  - 50,5\end{array}\)

Mà \(x\in Z\) nên không có $x$ thỏa mãn.