Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước. Vậy có duy nhất 1 đường thẳng đi qua hai điểm A và B.
Em hãy chọn phát biểu sai trong các phát biểu sau:
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau (đúng loại A)
+ \(\widehat A\) được gọi là góc tù nếu \(\widehat A > {90^0}\) (sai vì \(\widehat A\) được gọi là góc tù nếu \({90^0} < \widehat A < {180^0}\), chọn B)
+ Nếu tia Ot là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)(đúng loại C)
+ Tam giác MNP là hình gồm các đoạn thẳng MN, MP và NP khi ba điểm M, N, P không thẳng hàng. (đúng loại D)
Cho hình vẽ. Em hãy chọn đáp án đúng.

Quan sát hình vẽ ta thấy điểm B nằm giữa hai điểm A và C.
Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

Nhận xét:
+ Đáp án A: Hai tia NM và MP là hai tia không chung gốc nên loại đáp án A.
+ Đáp án B: Hai tia MP và NP là hai tia không chung gốc nên loại đáp án B.
+ Đáp án C: thấy hai tia PN và PM là hai tia cùng chung gốc P và tạo thành nửa đường thẳng nên hai tia PN và PM là hai tia trùng nhau, do đó chọn đáp án C.
+ Đáp án D: Hai tia MN và MP là hai tia chung gốc nhưng tạo thành một đường thẳng nên hai tia MN và MP là hai tia đối nhau, do đó loại đáp án D.
Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:

Hình vẽ trên có các tia chung gốc B là: BA, Bx, By, BC và BD. Vậy có tất cả 5 tia chung gốc B.
Cho ba điểm không thẳng hàng $O, A, B.$ Tia $Ox$ nằm giữa hai tia $OA, OB$ khi và chỉ khi tia $Ox$ cắt
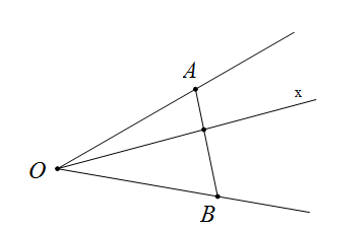
Tia $Ox$ nằm giữa hai tia $OA$ và $OB$ khi tia $Ox$ cắt đoạn thẳng $AB$
Cho hình vẽ sau. Chọn câu đúng.
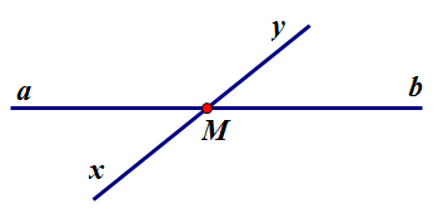
Ta thấy hai đường thẳng xy và ab cắt nhau tại M nên đáp án C đúng.
Cho hình vẽ sau. Chọn câu đúng.
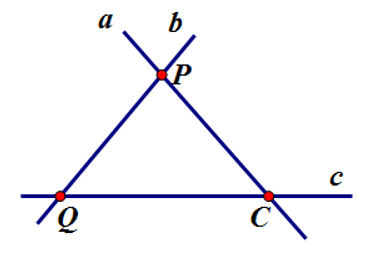
Từ hình vẽ ta thấy \(P \in a;P \in c\) nên đáp án A sai; \(Q \in b;Q \in c\) nên đáp án B đúng.
Hai đường thẳng a và c cắt nhau tại điểm C nên đáp án C sai.
Đáp án D sai vì ta thấy có ba cặp đường thẳng cắt nhau trên hình vẽ là a và c, a và b, b và c.
Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:
Với 3 đường thẳng phân biệt ta có các trường hợp sau:
+ Không có đường thẳng nào cắt nhau nên không có điểm chung.
+ Hai đường thẳng cắt nhau, đường thẳng còn lại không cắt hai đường thẳng đó, khi đó có 1 điểm chung.
+ Ba đường thẳng đó có đôi một cắt nhau thì có ba điểm chung.
Vậy không thể có trường hợp ba đường thẳng phân biệt bất kì mà có 4 điểm chung.
Cho hình vẽ. Em hãy chọn khẳng định sai:

Từ hình vẽ ta thấy các điểm M, N, I cùng thuộc một đường thẳng.
+) Hai tia NM và NI đối nhau vì chúng chung gốc N và tạo thành một đường thẳng, từ đó loại đáp án A.
+) Hai tia IN và IM trùng nhau vì chúng chung gốc I và có thêm điểm chung là N, từ đó loại đáp án B.
+) Hai tia MN và MI trùng nhau vì chúng chung gốc M và có thêm điểm chung là N, từ đó loại đáp án C.
+) Hai tia MN và NI không trùng nhau vì chúng không chung gốc.
Cho L là điểm nằm giữa hai điểm I và K. Biết $IL = 2cm,{\rm{ }}LK = 5cm.$ Độ dài của đoạn thẳng IK là:

Vì L nằm giữa I và K nên ta có:\(IL + LK = IK \Rightarrow IK = 2 + 5 = 7cm\)
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
Điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IL + IK = LK\) nên \(4 + IK = 5 \Rightarrow IK = 5 - 4 = 1cm\)
Vậy điều kiện để điểm I nằm giữa hai điểm L và K là $IK = 1cm\;$
Cho điểm I thuộc đoạn thẳng AB. Biết $AI = 5cm,AB = 8cm.$ Tính độ dài $BI.$
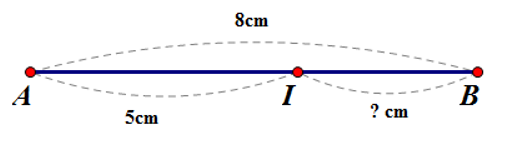
Vì điểm Ihuộc đoạn thẳng AB; $AI = 5cm,{\rm{ }}AB = 8cm$ mà $5cm < 8cm$ nên $AI < AB\;$
Suy ra điểm I nằm giữa hai điểm A và B
$ \Rightarrow AI + IB = AB \Rightarrow 4cm + IB = 7cm \Rightarrow IB = 7cm - 4cm = 3cm$
Cho đoạn thẳng $BC = 32cm.$ Gọi G là trung điểm của đoạn thẳng $BC,{\rm{ }}H$ là trung điểm của đoạn thẳng $GC.$ Khi đó, độ dài của đoạn thẳng BH là

Vì G là trung điểm của đoạn thẳng BC nên ${\rm{BG = }}\,GC = \dfrac{1}{2}BC = \dfrac{1}{2} \cdot 32 = 16\,cm$.
Vì H là trung điểm của đoạn thẳng GC nên ${\rm{GH }} = HC = {\rm{ }}\dfrac{1}{2}GC = \dfrac{1}{2} \cdot 16 = 8\,cm$.
Ta có G thuộc đoạn thẳng BC nên GB và GC là hai tia đối nhau. (1)
Vì H là trung điểm của GC nên H thuộc GC (2)
Từ (1) và (2) suy ra G là điểm nằm giữa hai điểm B và H.
\(\begin{array}{l} \Rightarrow BG + GH = BH\\ \Rightarrow 16 + 8 = BH\\ \Rightarrow BH = 24cm\end{array}\)
Lấy bốn điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:
Từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được các đường thẳng đi qua hai điểm bất kì như sau:
+ Với điểm M ta có thể nối với các điểm: N, P, Q, K để tạo thành 4 đường thẳng phân biệt.
+ Với điểm N ta có thể nối với các điểm: P, Q, K để tạo thành 3 đường thẳng phân biệt.
+ Với điểm P ta có thể nối với các điểm: Q, K để tạo thành 2 đường thẳng phân biệt.
+ Với điểm Q ta có thể nối với điểm K để tạo thành 1 đường thẳng .
Vậy từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được tất cả:
4 + 3 + 2 + 1 = 10 đường thẳng phân biệt.
Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?
Vì qua 2 điểm luôn vẽ được một đoạn thẳng
Nên qua 6 điểm vẽ được số đoạn thẳng là:
\(\dfrac{{6\left( {6 - 1} \right)}}{2} = 15\) (đoạn thẳng)
Cho M thuộc đoạn thẳng AB, $AM = 4cm,{\rm{ }}AB = 6cm.$ Gọi O là trung điểm của đoạn AB.
Tính $MO$.

+) Vì \(M \in AB\) nên M nằm giữa A và B
\( \Rightarrow AM + MB = AB \Rightarrow BM \)\(= AB - MB = 6 - 4 = 2cm.\)
+) Vì O là trung điểm của AB nên: \(AO = OB = \dfrac{{AB}}{2} \)\(= \dfrac{6}{2} = 3cm\)
Vì \(O \in AB\), \(M \in AB\) và \(AO < AM (3cm < 4cm)\) nên O nằm giữa A và M suy ra:
\(AO + OM = AM \Rightarrow OM\)\( = AM - AO = 4 - 3 = 1cm\)
Cho M thuộc đoạn thẳng AB, $AM = 4cm,{\rm{ }}AB = 6cm.$ Gọi O là trung điểm của đoạn AB.
Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.

+ ) Vì \(O \in AB\), \(I \in AB\) và AO < AI (3cm < 3,5cm) nên O nằm giữa A và I suy ra:
\(AO + OI = AI \)\(\Rightarrow OI = AI - AO = 3,5 - 3 = 0,5cm\) (1)
Vì \(I \in AB\), \(M \in AB\) và AI < AM (3,5cm < 4cm) nên I nằm giữa A và M suy ra:
\(AI + IM = AM \Rightarrow IM = AM - AI = 4 - 3,5 = 0,5cm\)(2)
Từ (1) và (2) suy ra $OI = IM$ . (3)
Vì O nằm giữa A và I nên A và O nằm cùng phía đối với I . Mà I nằm giữa A và M nên A và M nằm khác phía đối với I \( \Rightarrow \) O và M nằm khác phía đối với I suy ra I nằm giữa M và O (4)
Từ (3) và (4) suy ra I là trung điểm của OM.
+) Vì P là trung điểm của AO nên: \(OP = AP = \dfrac{{AO}}{2} = \dfrac{3}{2} = 1,5cm\)
Vì $\left\{ \begin{array}{l}O,M \in AB\\AO < AM\left( {3cm < 4cm} \right)\end{array} \right. \Rightarrow $ O nằm giữa A và M
Suy ra A và M nằm khác phía đối với O
Vì P là trung điểm của AO nên A, P cùng phía đối với O.
Vì I là trung điểm của OM nên I, M cùng phía đối với O.
Từ đó suy ra I nằm giữa O và P \( \Rightarrow OP + IO = IP \)\(\Rightarrow IP = 1,5 + 0,5 = 2cm\)
Cho \(100\) tia gồm \(O{x_2},O{x_3},....,O{x_{99}}\) nằm giữa hai tia \(O{x_1}\) và \(O{x_{100}}\). Hỏi có bao nhiêu góc được tạo thành?
- \(O{x_1}\) cùng với các tia \(O{x_2},O{x_3},....,O{x_{100}}\) tạo thành \(99\) góc.
- \(O{x_2}\) cùng với các tia \(O{x_3},....,O{x_{100}}\) tạo thành 98 góc.
- \(O{x_3}\) cùng với các tia \(O{x_4},O{x_5},....,O{x_{100}}\) tạo thành \(97\)góc.
…………
\(O{x_{99}}\) cùng tia \(O{x_{100}}\) tạo thành 1 góc.
Vậy ta có tất cả: \(1 + 2 + 3 + ... + 99 = \dfrac{{100.99}}{2} = 4950\) góc.
Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?
Giả sử trong 24 điểm không có 3 điểm nào thẳng hàng tất cả vẽ được:
$\dfrac{{24.(24 - 1)}}{2} = 276$ (đường thẳng)
Qua 6 điểm thẳng hàng vẽ được số đường thẳng là: $\dfrac{{6.(6 - 1)}}{2} = 15$ (đường thẳng)
Nhưng qua 6 điểm thẳng hàng chỉ vẽ được một đường thẳng
Nên qua 24 điểm trong đó có 6 điểm thẳng hàng vẽ được:
$276 - 15 + 1 = 262$ (đường thẳng)

