Phương pháp giải
1. VA CHẠM THEO PHƯƠNG NGANG

Vật m chuyển động với vận tốc v0 đến va chạm vào vật M đang đứng yên.
- Va chạm mềm: \(m{v_0} = (m + M)V \Rightarrow V = \frac{1}{{1 + \frac{M}{m}}}{v_0}\)
V: vận tốc của hệ hai vật M+m ở vị trí cân bằng
Nếu sau va chạm cả hai vật dao động điều hòa thì tần số và biên độ dao động của con lắc lò xo:
\(\omega = \sqrt {\frac{k}{{m + M}}} ,A = \frac{V}{\omega }\)
- Va chạm đàn hồi: \(\left\{ \begin{array}{l}m{v_0} = mv + MV\\\frac{1}{2}mv_0^2 = \frac{1}{2}m{v^2} + \frac{1}{2}M{V^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}V = \frac{2}{{1 + \frac{M}{m}}}{v_0}\\v = \frac{{1 - \frac{M}{m}}}{{1 + \frac{M}{m}}}{v_0}\end{array} \right.\)
V: vận tốc của M ở vị trí cân bằng
Nếu sau va chạm M dao động điều hòa: \(\omega = \sqrt {\frac{k}{M}} ,A = \frac{V}{\omega }\)
2. VA CHẠM THEO PHƯƠNG THẲNG ĐỨNG
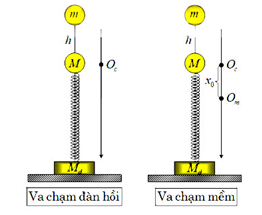
Tốc độ của m ngay trước va chạm: \({v_0} = \sqrt {2gh} \)
- Va chạm mềm:
+ Vị trí cân bằng mới thấp hơn vị trí cân bằng cũ đoạn \({x_0} = \frac{{mg}}{k}\)
+ Vận tốc của hệ sau va chạm: \(V = \frac{{m{v_0}}}{{m + M}}\)
+Biên độ sau va chạm: \(A = \sqrt {x_0^2 + \frac{{{V^2}}}{{{\omega ^2}}}} \)
- Xảy ra va chạm đúng lúc vật đến vị trí cao nhất thì sau va chạm: vật có li độ so với VTCB mới (A0+x0), biên độ mới \(A = \sqrt {{{({A_0} + {x_0})}^2} + \frac{{{V^2}}}{{{\omega ^2}}}} \)
- Xảy ra va chạm đúng lúc vật đến vị trí thấp nhất thì sau va chạm: vật có li độ so với VTCB mới (A0-x0), biên độ mới \(A = \sqrt {{{({A_0} - {x_0})}^2} + \frac{{{V^2}}}{{{\omega ^2}}}} \)
- Va chạm đàn hồi:
+ \(V = \frac{{2m{v_0}}}{{m + M}} \Rightarrow A = \frac{V}{\omega },\omega = \sqrt {\frac{k}{M}} \)
+ Nếu đúng lúc vật đến vị trí biên (x=±A0) thì xảy ra va chạm: \(A = \sqrt {x_0^2 + \frac{{{V^2}}}{{{\omega ^2}}}} \)
3. SAU VA CHẠM ĐÀN HỒI HAI VẬT TÁCH RỜI Ở VỊ TRÍ CÂN BẰNG
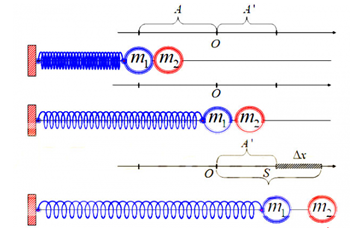
- Giai đoạn 1: Cả hai vật cùng dao động với biên độ A, tần số góc \(\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} \) và tốc độ cực đại v0=ωA
- Giai đoạn 2: Nếu đến VTCB m2 tách ra khỏi m1 thì m1 dao động điều hòa với tần số góc và biên độ:
\(\omega = \sqrt {\frac{k}{{{m_1}}}} ,A' = \frac{{{v_0}}}{\omega } = A\sqrt {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \)
(Vì tốc độ cực đại không đổi vẫn là vo)
m2 chuyển động thẳng đều với vận tốc v0 và khi đến vị trí biên dương (lần 1) thì m2 đi được quãng đường: \(S = {v_0}\frac{{T'}}{4} = \frac{1}{2}\pi A\sqrt {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \)
Lúc này khoảng cách giữa hai vật: \(\Delta x = S - A'\)

