I – TÁN SẮC ÁNH SÁNG
Sự tán sắc ánh sáng là sự phân tách một chùm ánh sáng phức tạp thành các chùm sáng đơn sắc
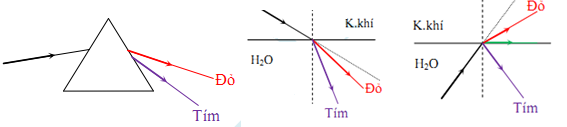
- Ánh sáng đơn sắc: là ánh sáng không bị tán sắc khi đi qua lăng kính
- Ánh sáng trắng: là hỗn hợp của ánh sáng đơn sắc có màu từ Đỏ đến Tím
- Chiết suất của thủy tinh đối với các ánh sáng đơn sắc có màu khác nhau thì khác nhau: \(n = \dfrac{c}{v}\)
- Vận tốc truyền ánh sáng trong các môi trường của ánh sáng đơn sắc là khác nhau:
+ vđỏ > vcam > vvàng > vlục > vlam > vchàm > vtím
+ nđỏ < ncam < nvàng < nlục < nlam < nchàm < ntím
+ Dđỏ < Dcam < Dvàng < Dlục < Dlam < Dchàm <Dtím
Chú ý:
+ Khi ánh sáng truyền từ môi trường này sang môi trường khác thì tần số không thay đổi, bước sóng và vận tốc ánh sáng thay đổi
+ Bước sóng trong môi trường có chiết suất n: \(\lambda = \dfrac{{{\lambda _{ck}}}}{n}\)
II – GIAO THOA ÁNH SÁNG
Hiện tượng giao thoa ánh sáng là bằng chứng thực nghiệm khẳng định ánh sáng có tính chất sóng.
1. Giao thoa ánh sáng đơn sắc
- Khoảng vân: \(i = \dfrac{{\lambda D}}{a}\)
- Vị trí vân sáng trên màn: \(\left\{ \begin{array}{l}{d_2} - {d_1} = k\lambda \\{x_s} = ki = k\dfrac{{\lambda D}}{a}\end{array} \right.\)
- Vị trí vân tối trên màn: \(\left\{ \begin{array}{l}{d_2} - {d_1} = \left( {k + \dfrac{1}{2}} \right)\lambda \\{x_t} = \left( {k + \dfrac{1}{2}} \right)i = \left( {k + \dfrac{1}{2}} \right)\dfrac{{\lambda D}}{a}\end{array} \right.\)
- Số vân sáng – tối trên màn:
+ Cách giải đại số:
\( - \dfrac{L}{2} \le {x_M} \le \dfrac{L}{2} \leftrightarrow \left\langle \begin{array}{l} - \dfrac{L}{2} \le ki \le \dfrac{L}{2} \to \left\{ \begin{array}{l} - \dfrac{L}{{2i}} \le k \le \dfrac{L}{{2i}}\\k \in Z\end{array} \right.{\rm{ (1)}}\\ - \dfrac{L}{2} \le (k + 0,5) \le \dfrac{L}{2} \to \left\{ \begin{array}{l} - \dfrac{1}{2} - \dfrac{L}{{2i}} \le k \le - \dfrac{1}{2} + \dfrac{L}{{2i}}\\k \in Z\end{array} \right.{\rm{ (2)}}\end{array} \right.\)
(1): xác định số vân sáng
(2): xác định số vân tối
+ Cách giải nhanh:
* Số vân sáng: \({N_S} = 2\left[ {\dfrac{L}{{2i}}} \right] + 1\) , trong đó: \(\left[ {\dfrac{L}{{2i}}} \right]\) là phần nguyên của \(\dfrac{L}{{2i}}\)
Ví dụ: \(\left[ {\dfrac{L}{{2i}}} \right] = \left[ {3,7} \right] = 3\)
* Số vân tối:
Nếu phần thập phân của \(\dfrac{L}{{2i}} < 0,5\)thì \({N_t} = {\rm{ }}{N_S} - {\rm{ }}1\)
Nếu phần thập phân của \(\dfrac{L}{{2i}} \ge 0,5\)thì \({N_t} = {\rm{ }}{N_S} + {\rm{ }}1\)
2. Giao thoa 2, 3 ánh sáng
- Khi 2 vân sáng của hai bức xạ trùng nhau (vân sáng cùng màu với vân sáng trung tâm) thì: \({x_{{S_1}}} = {x_{{S_2}}} \to {k_1}\dfrac{{{\lambda _1}D}}{a} = {k_2}\dfrac{{{\lambda _2}D}}{a} \to {k_1}{\lambda _1} = {k_2}{\lambda _2}\)
\( \to \dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}}\) (Phân số tối giản)
- Vị trí vân sáng trùng nhau của 3 bức xạ:
\( \to {x_1} = {x_2} = {x_3} \leftrightarrow {k_1}{\lambda _1} = {\rm{ }}{k_2}{\lambda _2} = {\rm{ }}{k_3}{\lambda _3}\)
3. Giao thoa ánh sáng trắng
Cho vị trí x bất kì:
+ Xét tại x có số vân sáng trùng nhau:
\(\left\{ \begin{array}{l}x = k\dfrac{{\lambda D}}{a}\\{\lambda _{\min }} \le \lambda \le {\lambda _{{\rm{max}}}}\end{array} \right. \to \dfrac{{{\rm{ax}}}}{{{\lambda _{{\rm{max}}}}D}} \le k \le \dfrac{{{\rm{ax}}}}{{{\lambda _{\min }}D}}\)
+ Xét tại x có số vân tối trùng nhau:
\(\left\{ \begin{array}{l}x = (k + \dfrac{1}{2})\dfrac{{\lambda D}}{a}\\{\lambda _{\min }} \le \lambda \le {\lambda _{{\rm{max}}}}\end{array} \right. \to \dfrac{{{\rm{ax}}}}{{{\lambda _{{\rm{max}}}}D}} \le k + \dfrac{1}{2} \le \dfrac{{{\rm{ax}}}}{{{\lambda _{\min }}D}}\)
- Bề rộng quang phổ bậc k:
\(\Delta x = {x_{{d_k}}} - {x_{{t_k}}} = k\dfrac{{{\lambda _d}D}}{a} - k\dfrac{{{\lambda _t}D}}{a} = ({\lambda _d} - {\lambda _t})k\dfrac{D}{a}\)
- Sự chồng chập quang phổ:
Đoạn chồng chập quang phổ bậc n với quang phổ bậc k (k<n)
\(\Delta x = {x_{{d_k}}} - {x_{{t_n}}} = k\dfrac{{{\lambda _d}D}}{a} - n\dfrac{{{\lambda _t}D}}{a} = (k{\lambda _d} - n{\lambda _t})\dfrac{D}{a}\)
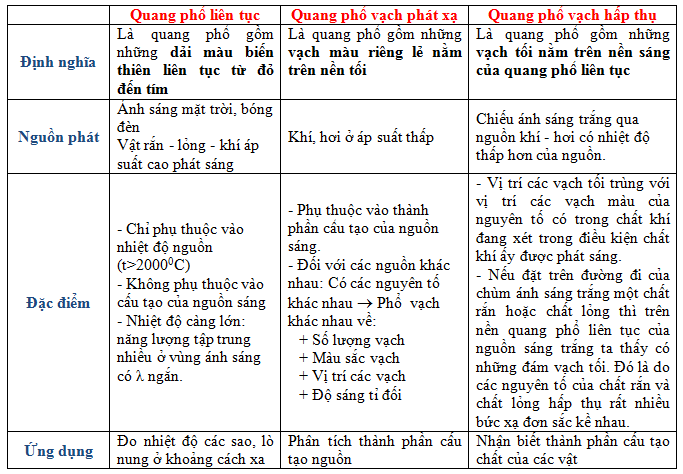
III – CÁC LOẠI QUANG PHỔ
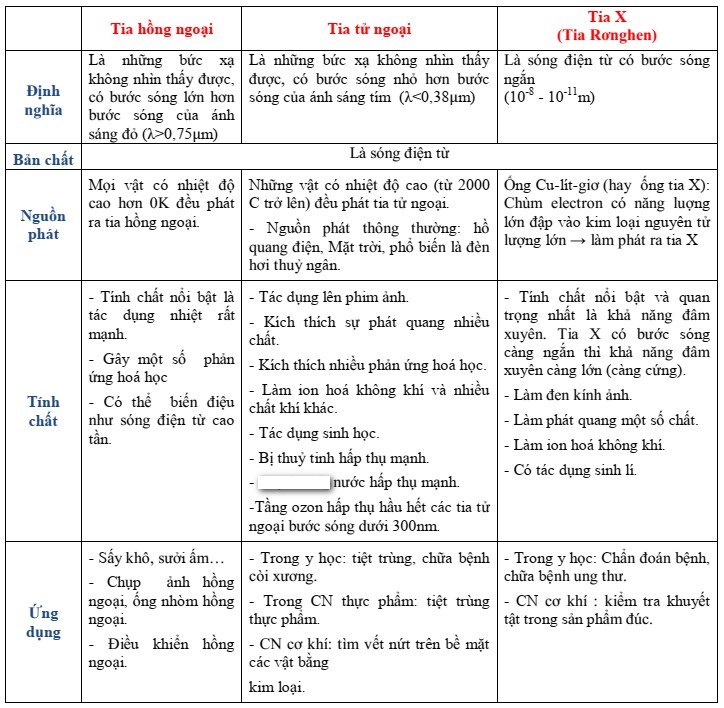
IV – CÁC LOẠI TIA
V – THANG SÓNG ĐIỆN TỪ
