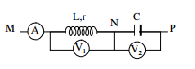
Sử dụng giải các bài toán liên quan đến sự lệch pha giữa các điện áp.
1. PHƯƠNG PHÁP
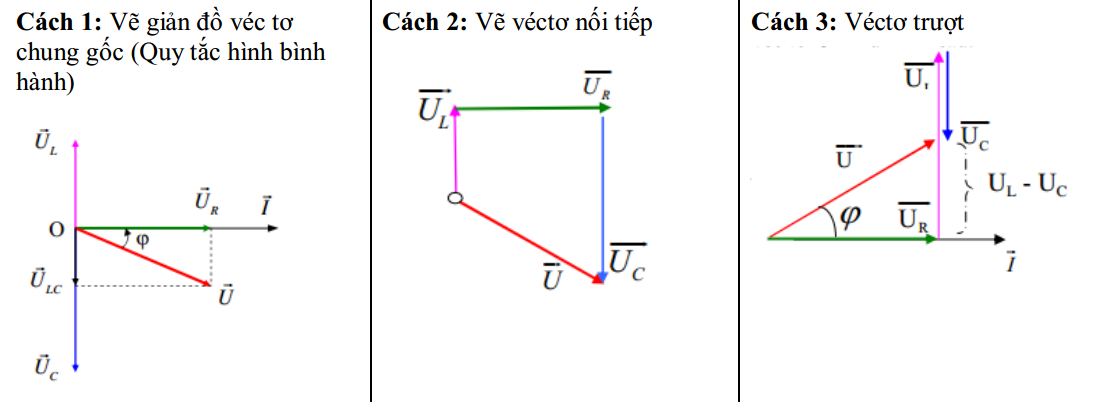
2. MỘT SỐ ĐỊNH LÍ TRONG TAM GIÁC THƯỜNG DÙNG
Tùy vào từng bài cụ thể, có thể vẽ các véctơ điện áp nối tiếp nhau dựa theo thứ tự của từng mạch điện hoặc vẽ chung gốc. Muốn có mối liên hệ của đại lượng cần tìm và đại lượng đã cho, thường dùng một số liên hệ sau:
- Nếu là tam giác thường:
- Định lí hàm số cosin: \({a^2} = {b^2} + {c^2} - 2bc.c{\rm{osA}}\)
- Định lí hàm số sin: \(\frac{a}{{{\mathop{\rm sinA}\nolimits} }} = \frac{b}{{{\mathop{\rm sinB}\nolimits} }} = \frac{c}{{{\mathop{\rm sinC}\nolimits} }}\)
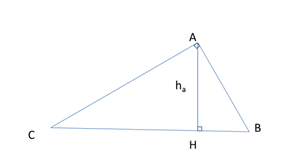
- Nếu là tam giác vuông:
- Định lí hàm sin, cos, tan, cotg
- Định lí pitago: \(B{C^2} = A{B^2} + A{C^2}\)
- \(\frac{1}{{h_a^2}} = \frac{1}{{A{C^2}}} + \frac{1}{{A{B^2}}}\)
- \(A{H^2} = HC.HB\)
- \(A{C^2} = CH.CB\)
- \(AC.AB = AH.CB\)
3. VÍ DỤ
Ví dụ: Cho mạch điện xoay chiều như hình vẽ, cuộn dây thuần cảm L, tụ điện có điện dung C, điện trở có giá trị R. Hai đầu A, B duy trì một điện áp \(u = 100\sqrt 2 {\rm{cos}}\left( {100\pi t} \right)V\). Cường độ dòng điện chạy trong mạch có giá trị hiệu dụng là 0,5A. Biết điên áp giữa hai điểm A, M sớm pha hơn dòng điện một góc \(\frac{\pi }{6}ra{\rm{d}}\) . Điện áp giữa hai điểm M, B chậm pha hơn điện áp giữa 2 đầu AB một góc \(\frac{\pi }{6}ra{\rm{d}}\).
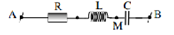
a. Tìm R, ZC?
b. Viết biểu thức cường độ dòng điện trong mạch?
c. Viết biểu thức điện áp AM?
Lời giải:
Chọn trục dòng điện làm trục pha
Theo bài ra uAM sớm pha \(\frac{\pi }{6}\)so với cường độ dòng điện, uMB chậm pha hơn uAB một góc \(\frac{\pi }{6}\), mà uMB lại chậm pha so với i một góc \(\frac{\pi }{2}\)nên uAB chậm pha \(\frac{\pi }{3}\)so với dòng điện
=> Ta có giản đồ véctơ:
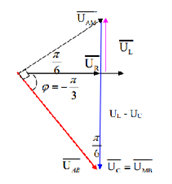
Từ giản đồ véctơ, ta có:
\({U_{AM}} = {U_{AB}}.\tan \frac{\pi }{6} = \frac{{100}}{{\sqrt 3 }}V\)
\({U_{MB}} = {U_C} = {U_{AB}}.\cos \frac{\pi }{6} = 100.\frac{{\sqrt 3 }}{2} = 50\sqrt 3 V\)
\({U_R} = {U_{AM}}.\cos \frac{\pi }{6} = 50V\)
a. Ta có: \(R = \frac{{{U_R}}}{I} = \frac{{50}}{{0,5}} = 100\Omega \)
\({Z_C} = \frac{{{U_C}}}{I} = \frac{{50\sqrt 3 }}{{0,5}} = 100\sqrt 3 \)
b. \({I_0} = 0,5\sqrt 2 A\)
Độ lệch pha của u so với i: \(\varphi = {\varphi _u} - {\varphi _i} = - \frac{\pi }{3} \to {\varphi _i} = {\varphi _u} + \frac{\pi }{3} = \frac{\pi }{3}\)
=> Biểu thức của i: \(i = 0,5\sqrt 2 {\rm{cos}}\left( {100\pi t + \frac{\pi }{3}} \right)A\)
c. \({U_{0{\rm{A}}M}} = {U_{{\rm{A}}M}}\sqrt 2 = 100\sqrt {\frac{2}{3}} V\)
Độ lệch pha của uAM so với i : \({\varphi _{AM}} - {\varphi _i} = \frac{\pi }{6} \to {\varphi _{AM}} = \frac{\pi }{6} + {\varphi _i} = \frac{\pi }{6} + \frac{\pi }{3} = \frac{\pi }{2}\)
=> Biểu thức của uAM: \({u_{AM}} = 100\sqrt {\frac{2}{3}} {\rm{cos}}\left( {100\pi t + \frac{\pi }{2}} \right)V\)
