1. \(\omega \) THAY ĐỔI ĐỂ XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG ĐIỆN: \({Z_{min}},{\rm{ }}{I_{max}},{\rm{ }}{U_{Rmax}},{\rm{ }}{P_{ABmax}},{\rm{ }}cos\varphi \) CỰC ĐẠI
\({Z_L} = {Z_C} \to {\omega ^2} = \frac{1}{{LC}}{\rm{ hay }}\omega = \frac{1}{{\sqrt {LC} }}\)
Khi đó:
\({Z_{\min }} = R,{\rm{ }}{I_{{\rm{max}}}} = \dfrac{U}{R},{\rm{ }}{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\)
+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch
\({U_L} = {U_C} \to U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} = {U_R}\)
+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: \(\varphi = 0\)
2. \(\omega \) THAY ĐỔI ĐỂ UCMAX
\({U_C} = I{Z_C} = \dfrac{{U{Z_C}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{U}{{\omega C\sqrt {{R^2} + {\omega ^2}{L^2} - 2\dfrac{L}{C} + \dfrac{1}{{{\omega ^2}{C^2}}}} }} = \dfrac{U}{{C\sqrt {{\omega ^4}{L^2} + ({R^2} - 2\dfrac{L}{C}){\omega ^2} + \dfrac{1}{{{C^2}}}} }}\)
UC max <=> mẫu min
Đặt \({\omega ^2} = x\) , \( \to {x^2}{L^2} + ({R^2} - 2\dfrac{L}{C})x + \dfrac{1}{{{C^2}}} = y\)
\({y_{\min }} \leftrightarrow x = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{1}{{LC}} - \dfrac{{{R^2}}}{{2{L^2}}},{y_{\min }} = - \dfrac{\Delta }{{4{\rm{a}}}} = \dfrac{{{R^2}}}{{LC}} - \dfrac{{{R^4}}}{{2{L^2}}}\)
Khi đó ta có:
\(\begin{array}{l}{Z_L} = \omega L = \sqrt {\dfrac{1}{{LC}} - \dfrac{{{R^2}}}{{2{L^2}}}} L \to Z_L^2 = \dfrac{L}{C} - \dfrac{{{R^2}}}{2}\\ \leftrightarrow Z_L^2 = {Z_L}{Z_C} - \dfrac{{{R^2}}}{2}\\ \to \dfrac{{{R^2}}}{2} = {Z_L}\left( {{Z_C} - {Z_L}} \right)\\ \to \dfrac{{{Z_L}}}{R}\dfrac{{\left( {{Z_C} - {Z_L}} \right)}}{R} = \dfrac{1}{2} \leftrightarrow \tan {\varphi _{RL}}\tan \varphi = -\dfrac{1}{2}\end{array}\)
Vẽ giản đồ ta được:
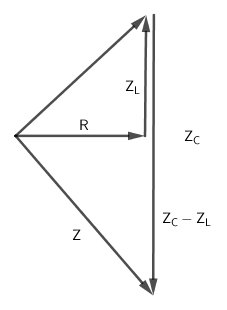
Từ giản đồ, ta có:
\(\begin{array}{l}{Z^2} = {R^2} + {\left( {{Z_C} - {Z_L}} \right)^2} = 2{Z_L}\left( {{Z_C} - {Z_L}} \right) + {\left( {{Z_C} - {Z_L}} \right)^2}\\ \leftrightarrow {Z^2} = Z_C^2 - Z_L^2\end{array}\)
Kết luận: \(\omega \) biên thiên để \({U_{{C_{max}}}}\), khi đó:
\({U_{Cm{\rm{ax}}}} = \dfrac{{2UL}}{{R\sqrt {4LC - {R^2}{C^2}} }},{\rm{ }}{\omega ^2}{\rm{ = }}\dfrac{1}{{LC}} - \dfrac{{{R^2}}}{{2{L^2}}}\)
\(\tan {\varphi _{RL}}\tan \varphi = -\dfrac{1}{2}\) và \(Z_C^2 = {Z^2} + Z_L^2\)
3. \(\omega \) THAY ĐỔI ĐỂ ULMAX
\({U_L} = I{Z_L} = \dfrac{{U{Z_L}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{{U\omega L}}{{\sqrt {{R^2} + {\omega ^2}{L^2} - 2\dfrac{L}{C} + \dfrac{1}{{{\omega ^2}{C^2}}}} }} = \dfrac{{UL}}{{\sqrt {{L^2} + \dfrac{{({R^2} - 2\dfrac{L}{C})}}{{{\omega ^2}}} + \dfrac{1}{{{\omega ^4}{C^2}}}} }}\)
\({U_{L{\rm{ }}max}}\) <=> mẫu min
Đặt \(\dfrac{1}{{{\omega ^2}}} = x\), \( \to {L^2} + ({R^2} - 2\dfrac{L}{C})x + {x^2}\dfrac{1}{{{C^2}}} = y\)
\({y_{\min }} \leftrightarrow x = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{{2LC - {R^2}{C^2}}}{2},{y_{\min }} = - \dfrac{\Delta }{{4{\rm{a}}}} = \dfrac{{4L{{\rm{R}}^2} - {R^4}C}}{4}C\)
Khi đó ta có:
\(\begin{array}{l} \to Z_C^2 = \dfrac{1}{{{\omega ^2}{C^2}}} = \dfrac{1}{{\dfrac{2}{{2LC - {R^2}{C^2}}}{C^2}}} = \dfrac{L}{C} - \dfrac{{{R^2}}}{2}\\ \leftrightarrow Z_C^2 = {Z_L}{Z_C} - \dfrac{{{R^2}}}{2}\\ \leftrightarrow \dfrac{{{R^2}}}{2} = {Z_C}\left( {{Z_L} - {Z_C}} \right) \leftrightarrow \dfrac{{{Z_C}}}{R}\dfrac{{\left( {{Z_L} - {Z_C}} \right)}}{R} = \dfrac{1}{2}\\ \leftrightarrow \tan {\varphi _{RC}}\tan \varphi = -\dfrac{1}{2}\end{array}\)
Vẽ giản đồ ta được:
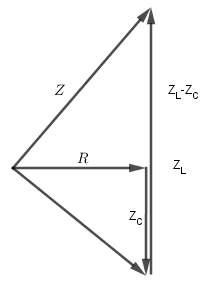
Từ giản đồ, ta có:
\(\begin{array}{l}{Z^2} = {R^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = 2{Z_C}\left( {{Z_L} - {Z_C}} \right) + {\left( {{Z_C} - {Z_L}} \right)^2}\\ \leftrightarrow {Z^2} = Z_L^2 - Z_C^2\end{array}\)
Kết luận: \({U_{Lm{\rm{ax}}}} = \dfrac{{2UL}}{{R\sqrt {4LC - {R^2}{C^2}} }},{\rm{ }}{\omega ^2}{\rm{ = }}\dfrac{2}{{2LC - {R^2}{C^2}}}\)
\(\tan {\varphi _{RC}}\tan \varphi =- \dfrac{1}{2}\) và \(Z_L^2 = {Z^2} + Z_C^2\)
Khi \(\omega \) thay đổi để \({U_{Cmax}},{\rm{ }}{U_{Lmax}}\)
\(\begin{array}{l}{U_{Cm{\rm{ax}}}} = {U_{Lm{\rm{ax}}}} = \dfrac{{2UL}}{{R\sqrt {4LC - {R^2}{C^2}} }}\\{\omega _L}.{\omega _C} = \dfrac{1}{{LC}} = \omega _0^2\end{array}\)
4. THAY ĐỔI \(f\) CÓ HAI GIÁ TRỊ \({f_{\bf{1}}} \ne {f_{\bf{2}}}\) BIẾT \({f_{\bf{1}}} + {f_{\bf{2}}} = {\rm{ }}{\bf{a}}\) VÀ CÙNG CÔNG SUẤT HOẶC CÙNG \({\bf{I}},{\bf{Z}},{\bf{cos}}\varphi ,{{\bf{U}}_{{\bf{R}}.}}\)
- Hai giá trị tần số làm cho mạch có cùng công suất nên:
\(\begin{array}{l}{P_1} = {P_2} \Leftrightarrow I_1^2R = I_2^2R \Leftrightarrow I_1^2 = I_2^2\\ \to \dfrac{{{U^2}}}{{{R^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}} = \dfrac{{{U^2}}}{{{R^2} + {{({Z_{L2}} - {Z_{C2}})}^2}}}\\ \to {({Z_{L1}} - {Z_{C1}})^2} = {({Z_{L2}} - {Z_{C2}})^2} \to \left[ \begin{array}{l}{Z_{L1}} - {Z_{C1}} = {Z_{L2}} - {Z_{C2}}(loai)\\{Z_{L1}} - {Z_{C1}} = - ({Z_{L2}} - {Z_{C2}})\end{array} \right.\\ \to {Z_{L1}} + {Z_{L2}} = {Z_{C1}} + {Z_{C2}}) \to L({\omega _1} + {\omega _2}) = \dfrac{1}{C}(\dfrac{1}{{{\omega _1}}} + \dfrac{1}{{{\omega _2}}}) = \dfrac{1}{C}\dfrac{{{\omega _1} + {\omega _2}}}{{{\omega _1}{\omega _2}}}\\ \to {\omega _1}{\omega _2} = \dfrac{1}{{LC}} = \omega _0^2\end{array}\)
- Công thức trên áp dụng cho bài toán thay đổi f có cùng I, Z, cosφ, UR
Các hệ quả thu được:
- Cảm kháng và dung kháng trong hai trường hợp:
\({({Z_{L1}} - {Z_{C1}})^2} = {({Z_{L2}} - {Z_{C2}})^2}{\rm{ hay }}\left| {{Z_L} - {Z_C}} \right| = h/s \to \left| \begin{array}{l}{Z_{L1}} = {Z_{C2}}\\{Z_{L2}} = {Z_{C1}}\end{array} \right.\)
- Hệ số công suất trong hai trường hợp: \({\rm{cos}}{\varphi _1} = {\rm{cos}}{\varphi _2} = \dfrac{1}{{\sqrt {1 + k{{(\sqrt {\dfrac{{{\omega _1}}}{{{\omega _2}}}} - \sqrt {\dfrac{{{\omega _2}}}{{{\omega _1}}}} )}^2}} }}{\rm{ (}}\dfrac{L}{C} = k.{R^2})\)
- Cường độ dòng điện trong hai trường hợp: \({I_1} = {I_2} = \dfrac{{{I_{{\rm{max}}}}}}{n}\)
Điện trở của mạch được xác định: \(R = L\dfrac{{\left| {{\omega _1} - {\omega _2}} \right|}}{{\sqrt {{n^2} - 1} }} = \dfrac{{\left| {{\omega _1} - {\omega _2}} \right|}}{{{\omega _1}{\omega _2}C\sqrt {{n^2} - 1} }}\)

