1. DỊCH CHUYỂN NGUỒN SÁNG S
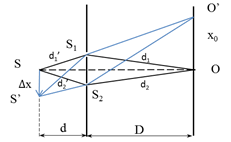
Quang trình: đường đi của ánh sáng.
\(\left\{ \begin{array}{l}{S_1}:{d_1}' + {d_1}\\{S_2}:{d_2}' + {d_2}\end{array} \right. \to \) Tại vị trí vân trung tâm: \({d_1}' + {\rm{ }}{d_1} = {\rm{ }}{d_2}{\rm{' }} + {\rm{ }}{d_2} \to \left( {{d_1}{\rm{' }} + {\rm{ }}{d_1}} \right) - \left( {{d_2}{\rm{' }} + {\rm{ }}{d_2}} \right){\rm{ }} = {\rm{ }}0 = 0\frac{{\lambda D}}{a}\)
=> Tại O là vân trung tâm
Dịch nguồn S một khoảng \(\Delta x \to {d_1}';{d_1}\) thay dổi => Vị trí vân trung tâm thay đổi
\(\begin{array}{l}{d_1}{\rm{' }} + {\rm{ }}{d_1} = {\rm{ }}{d_2}{\rm{' }} + {\rm{ }}{d_2} \to \left| {{d_1}' - {d_2}'} \right| = \left| {{d_1} - {d_2}} \right|\\ \leftrightarrow \frac{{a\Delta x}}{d} = \frac{{{\rm{a}}{{\rm{x}}_0}}}{D} \to {x_0} = \frac{{\Delta xD}}{d}\end{array}\)
2. ĐẶT TRƯỚC S1 (HOẶC S2) MỘT LƯỠNG CHẤT PHẲNG CÓ BỀ DÀY e VÀ CHIẾT SUẤT n
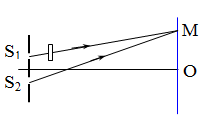
- Ta có:
- Vận tốc ánh sáng trong lưỡng chất phẳng: \(v = \frac{c}{n}\)
- Thời gian ánh sáng đi trong lưỡng chất phẳng: \(\Delta t = \frac{e}{v} = \frac{{en}}{c}\)
- Cũng trong thời gian ∆t đó thì ánh sáng đi ở môi trường ngoài 1 đoạn khác: \(\Delta x = c\Delta t = en\)
- Quang lộ: \({S_1}M = {d_1} + (n - 1)e\), \({S_2}M = {d_2} = {d_1}\)
=> Hiệu quang trình: \(\delta = {S_2}M - {S_1}M = {d_2}-{d_1}-\left( {n-1} \right)e\)
Mà: \({d_2}-{d_1} = \frac{{ax}}{D} \to \delta = \frac{{ax}}{D}-\left( {n-1} \right)e\)
Vân sáng trung tâm ứng với hiệu quang trình bằng \(\delta \)= 0.
\(\delta = \frac{{{\rm{ }}a{x_0}}}{D}-\left( {n-1} \right)e = 0\)
Hay: \({x_0} = \frac{{(n - 1)eD}}{a}\).
Hệ thống vân dịch chuyển về phía S1. Vì \({x_0} > 0\) .
