I. Sơ đồ tư duy công thức quãng đường
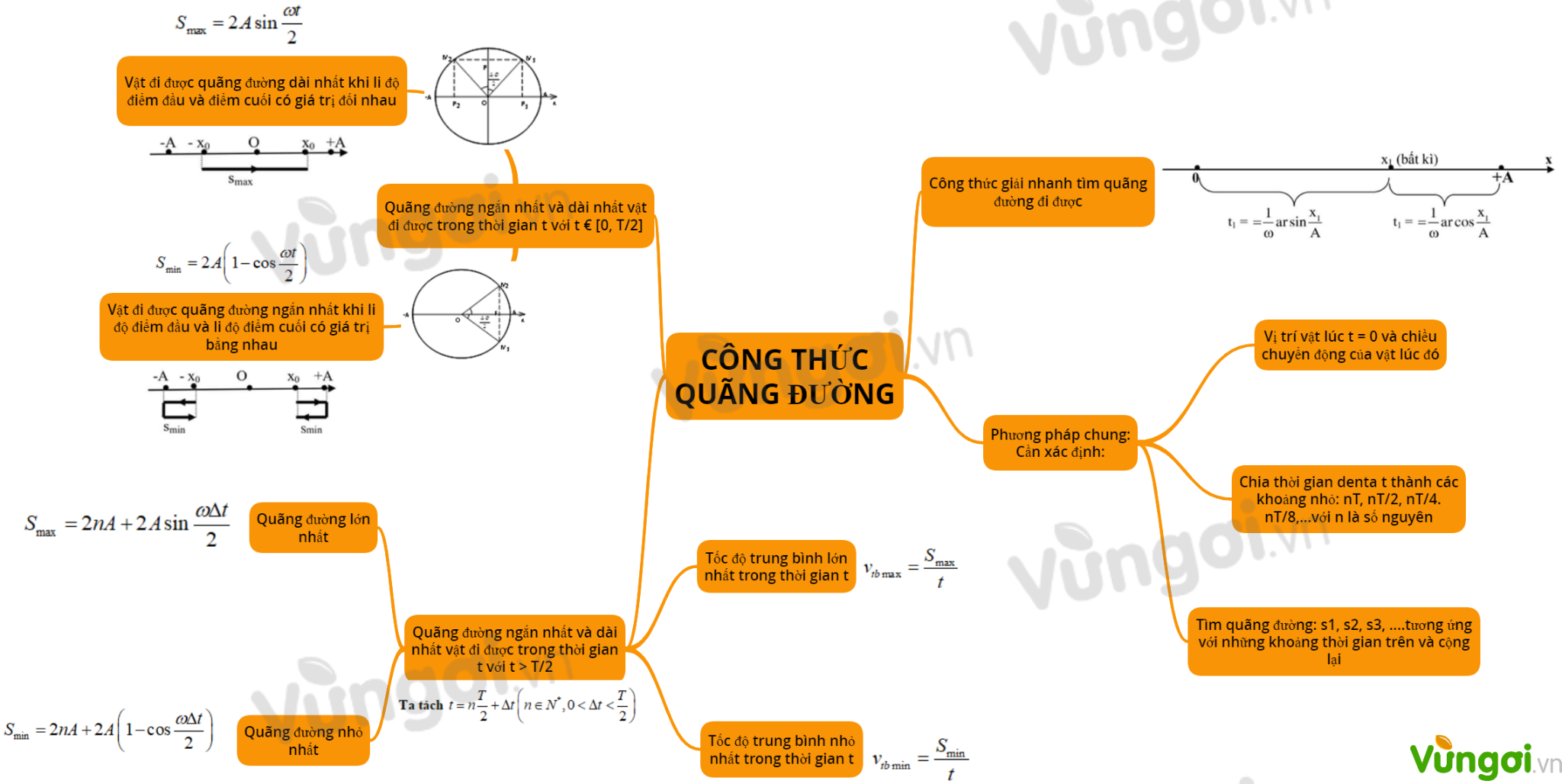
II. Ứng dụng vòng tròn lượng giác - Bài tập quãng đường - Tốc độ trung bình
I. DẠNG 1: QUÃNG ĐƯỜNG VẬT ĐI ĐƯỢC TỪ THỜI ĐIỂM T1 ĐẾN T2 - TỐC ĐỘ TRUNG BÌNH TRONG KHOẢNG THỜI GIAN ∆T
Chú ý:
+ Trong 1 chu kì, vật đi được quãng đường: \(S = 4A\)
+ Trong n chu kì, vật đi được quãng đường: \(S = 4nA\)
+ Trong \(\dfrac{1}{2}\) chu kì, vật đi được quãng đường: \(2A\)
Phương pháp giải:
- Cách 1: Phương pháp đại số
+ Bước 1: Xác định: \(\left\{ \begin{array}{l}{x_1} = {\rm{Aco}}{\mathop{\rm s}\nolimits} (\omega {t_1} + \varphi )\\{v_1} = - \omega A{\rm{sin}}(\omega {t_1} + \varphi )\end{array} \right.va \left\{ \begin{array}{l}{x_2} = {\rm{Aco}}{\mathop{\rm s}\nolimits} (\omega {t_2} + \varphi )\\{v_2} = - \omega A{\rm{sin}}(\omega {t_2} + \varphi )\end{array} \right.\)
(v1 và v2 chỉ cần xác định dấu)
+ Bước 2: Phân tích: t2 – t1 = nT/2 + Dt (n ÎN; 0 ≤ Dt < T/2)
+ Bước 3: Tính quãng đường:
Quãng đường đi được trong thời gian nT/2 là S1 = 2nA, trong thời gian Dt là S2.
Quãng đường tổng cộng là S = S1 + S2
( Tính S2 bằng cách định vị trí x1, x2 và chiều chuyển động của vật trên trục Ox)
- Cách 2: Phương pháp ứng dụng vòng tròn lượng giác
+ Bước 1: Phân tích: t2 – t1 = nT/4 + Dt (n ÎN; 0 ≤ Dt < T/4)
+ Bước 2: Tính quãng đường:
Quãng đường đi được trong thời gian nT/4 là S1 = nA, trong thời gian Dt là S2.
Quãng đường tổng cộng là S = S1 + S2
Tính S2 bằng cách xác định trên vòng tròn lượng giác (tọa độ và hướng của x1, x2)
- Tốc độ trung bình của vật đi từ thời điểm t1 đến t2:
\({v_{tb}} = \dfrac{S}{{{t_2} - {t_1}}}\) với S là quãng đường tính như trên.
Tốc độ trung bình trong 1 chu kì: \({v_{tb}} = \dfrac{{4A}}{T} = \dfrac{{4A}}{{\dfrac{{2\pi }}{\omega }}} = \dfrac{{2A\omega }}{\pi } = \dfrac{{2{v_{{\rm{max}}}}}}{\pi }\)
II. DẠNG 2: QUÃNG ĐƯỜNG LỚN NHẤT VÀ NHỎ NHẤT VẬT ĐI ĐƯỢC TRONG KHOẢNG THỜI GIAN ∆T - TỐC ĐỘ TRUNG BÌNH LỚN NHẤT VÀ NHỎ NHẤT TRONG KHOẢNG THỜI GIAN ∆T
Phương pháp giải:
Vật có vận tốc lớn nhất khi qua VTCB, nhỏ nhất khi qua vị trí biên nên trong cùng một khoảng thời gian quãng đường đi được càng lớn khi vật ở càng gần VTCB và càng nhỏ khi càng gần vị trí biên.
* Trường hợp: 0 < Dt < T/2
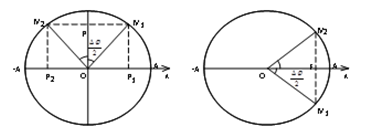
- Sử dụng mối liên hệ giữa dao động điều hoà và chuyển đường tròn đều.
+ Góc quét: Dj = wDt.
+ Quãng đường lớn nhất khi vật đi từ M1 đến M2 đối xứng qua trục sin (hình 1)
\({S_{M{\rm{ax}}}} = 2{\rm{A}}\sin \dfrac{{\Delta \varphi }}{2}\)
+ Quãng đường nhỏ nhất khi vật đi từ M1 đến M2 đối xứng qua trục cos (hình 2)
\({S_{Min}} = 2A(1 - c{\rm{os}}\dfrac{{\Delta \varphi }}{2})\)
* Trong trường hợp: Dt > T/2
Tách \(\Delta t = n\dfrac{T}{2} + \Delta t'\) trong đó \(n \in {N^*};0 < \Delta t' < \dfrac{T}{2}\)
+ Trong thời gian \(n\dfrac{T}{2}\) quãng đường luôn là 2nA
+ Trong thời gian Dt’ thì quãng đường lớn nhất, nhỏ nhất tính như trên.
+ Tốc độ trung bình lớn nhất và nhỏ nhất của trong khoảng thời gian Dt:
\({v_{tbM{\rm{ax}}}} = \dfrac{{{S_{M{\rm{ax}}}}}}{{\Delta t}}\) và \({v_{tbMin}} = \dfrac{{{S_{Min}}}}{{\Delta t}}\) với SMax; SMin tính như trên.

