Một vật dao động điều hòa theo phương trình \(x = 2cos(2πt + \dfrac{π}{4}) cm\). Tốc độ trung bình của vật trong khoảng thời gian từ \(t = 2s\) đến \(t = 4,875s\) là:
Trả lời bởi giáo viên
Hình vẽ :
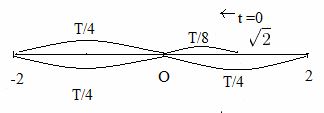
t = 0 =>
\(\left\{ \matrix{ x = \sqrt 2 \hfill \cr v < 0 \hfill \cr} \right.\)
\(\eqalign{ & \Delta t = \left| {{t_2} - {t_1}} \right| = 4,875 - 2 = 2,875{\rm{s}} \cr & \to {{\Delta t} \over T} = 2,875 \to \Delta t = 2,875T = 2T + {{7T} \over 8} \cr}\)
Theo hình vẽ : \(\Delta t = 2T + {T \over 8} = 2T + {T \over 8} + {T \over 4} + {T \over 4} + {T \over 4}\)
\(\eqalign{ & S = 2.4A + 3A + A{{\sqrt 2 } \over 2} = 22 + \sqrt 2 \cr & \to {v_{tb}} = {S \over {\Delta t}} = {{22 + \sqrt 2 } \over {2,875}} = 8,14cm/s \cr}\)
Hướng dẫn giải:
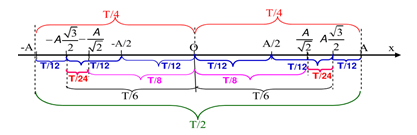
Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn