Câu hỏi:
2 năm trước
Một chất điểm dao động điều hòa có chu kì T. Trong khoảng thời gian ngắn nhất khi tốc độ của vật tăng từ 0 đến giá trị \(\dfrac{{\omega A}}{2}\) thì chất điểm có tốc độ trung bình là
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
+ Vị trí có tốc độ bằng 0: Vị trí biên
+ Vị trí có tốc độ \(\dfrac{{\omega A}}{2}\): \(\left| x \right| = \sqrt {{A^2} - \dfrac{{{{\left( {\dfrac{{\omega A}}{2}} \right)}^2}}}{{{\omega ^2}}}} = \dfrac{{A\sqrt 3 }}{2}\)
+ Thời gian ngắn nhất tốc độ của chất điểm tăng từ \(0 \to \dfrac{{A\omega }}{2}\) tương ứng là thời gian chất điểm đi từ \(A \to \dfrac{{A\sqrt 3 }}{2}\)
\(\Delta t = \dfrac{T}{{12}}\)
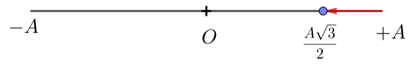
Quãng đường chất điểm đi được trong khoảng thời gian đó là: \(S = A - \dfrac{{A\sqrt 3 }}{2}\)
Tốc độ trung bình của chất điểm trong thời gian đó là: \({v_{tb}} = \dfrac{S}{{\Delta t}} = \dfrac{{A - \dfrac{{A\sqrt 3 }}{2}}}{{\dfrac{T}{{12}}}} = \dfrac{{6A\left( {2A - A\sqrt 3 } \right)}}{T}\)
Hướng dẫn giải:
+ Sử dụng công thức độc lập: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)
+ Sử dụng trục thời gian
+ Sử dụng công thức tính tốc độ trung bình: \({v_{tb}} = \dfrac{S}{t}\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
