1. CÔNG SUẤT CỦA MẠCH ĐIỆN XOAY CHIỀU.

- Công suất \(P = UIcos\varphi \) là công suất tiêu thụ trên toàn mạch điện, còn công suất \(P{\rm{ }} = {\rm{ }}{I^2}R\) là công suất tỏa nhiệt khi mạch có điện trở R, một phần công suất của mạch bị hao phí dưới dạng công suất tỏa nhiệt còn phần lớn là công suất có ích, khi đó \(P = {P_{co{\rm{ }}ich}} + {P_{hao{\rm{ phi}}}} \leftrightarrow UIcos\varphi = {\rm{ }}{P_{co{\rm{ i}}ch}} + {\rm{ }}{I^2}R\)
Mà \(I = \frac{P}{{Uc{\rm{os}}\varphi }} \to {P_{hao{\rm{ phi}}}} = {\left( {\frac{P}{{U\cos \varphi }}} \right)^2}R\)
Từ công thức tính công suất hao phí trên cho thấy để làm giảm đi công suất hao phí thì người ta tìm cách nâng cao hệ số công suất.
Và trong thực tế thì không sử dụng những thiết bị mà có hệ số công suất \(cos\varphi < {\rm{ }}0,85\)
- Hiệu suất của mạch điện (thiết bị tiêu thụ điện) là \({\bf{H}} = \frac{{{P_{co{\rm{ i}}ch}}}}{P}.100\% \)
2. HỆ SỐ CÔNG SUẤT.
- Khái niệm hệ số công suất
Đại lượng cosφ trong công thức tính công suất \({\bf{P}}{\rm{ }} = {\rm{ }}{\bf{UIcos}}\varphi \) được gọi là hệ số công suất của mạch điện xoay chiều.
- Công thức tính hệ số công suất
Theo khái niệm hệ số công suất ta có \({\rm{cos}}\varphi {\rm{ = }}\frac{P}{{UI}} = \frac{{2P}}{{{U_0}{I_0}}}\)
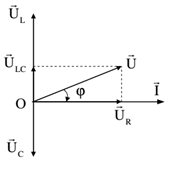
Theo giản đồ ta có:
\(cos\varphi = \frac{{{U_R}}}{U} = \frac{R}{Z}\)(*)
(*) là công thức tính giá trị của hệ số công suất trong các bài toán thường gặp.
- Biểu thức tính công suất khi mạch có R
Ta có \(P = UIcos\varphi = {\rm{ }}UI\frac{R}{Z} = \frac{U}{Z}IR = {I^2}R\)

