Chu kì dao động của con lắc đơn khi con lắc chịu thêm tác dụng của lực lạ là: \(T' = 2\pi \sqrt {\frac{l}{{g'}}} \)
Ta có: \(\overrightarrow {P'} = \overrightarrow P + \overrightarrow F \)
Trong đó: \(\overrightarrow {P'} \) : trọng lực biểu kiến (có vai trò như trọng lực), \(\overrightarrow P \) : trọng lực, \(\overrightarrow F \) lực lạ.
\( \to \overrightarrow {g'} = \overrightarrow g + \frac{{\overrightarrow F }}{m}\) : gia tốc trọng trường hiệu dụng hay gia tốc trọng trường biểu kiến.
I- CÁC LỰC LẠ THƯỜNG GẶP:
- Lực quán tính: \(\overrightarrow F = - m\overrightarrow a \), độ lớn F = ma ( \(\overrightarrow F \uparrow \downarrow \overrightarrow a \))
+ Chuyển động nhanh dần đều \(\overrightarrow a \uparrow \uparrow \overrightarrow v \) (\(\overrightarrow v \) có hướng chuyển động)
+ Chuyển động chậm dần đều \(\overrightarrow a \uparrow \downarrow \overrightarrow v \)
- Lực điện trường: \(\overrightarrow F = q\overrightarrow E \), độ lớn F = |q|E (Nếu q > 0 Þ \(\overrightarrow F \uparrow \uparrow \overrightarrow E \); còn nếu q < 0 Þ \(\overrightarrow F \uparrow \downarrow \overrightarrow E \))
- Lực đẩy Ácsimét: \(F = DgV\) (\(\overrightarrow F \)luông thẳng đứng hướng lên)
Trong đó:
- D là khối lượng riêng của chất lỏng hay chất khí.
- g là gia tốc rơi tự do.
- V là thể tích của phần vật chìm trong chất lỏng hay chất khí đó.
II- CÔNG THỨC ÁP DỤNG LÀM BÀI TẬP
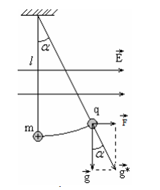
- \(\overrightarrow F \) có phương ngang: \(\overrightarrow F \bot \overrightarrow P \)
Tại VTCB dây treo lệch với phương thẳng đứng một góc có: \(\tan \alpha = \frac{F}{P}\)
Thì \(g' = \sqrt {{g^2} + {{(\frac{F}{m})}^2}} \)
Ví dụ:
- \(\overrightarrow F \)có phương thẳng đứng thì \(g' = g \pm \frac{F}{m}\)
- Nếu \(\overrightarrow F \) hướng xuống thì \(g' = g + \frac{F}{m}\)
- Nếu \(\overrightarrow F \) hướng lên thì \(g' = g - \frac{F}{m}\)
- \(\overrightarrow F \)có hướng xiên:
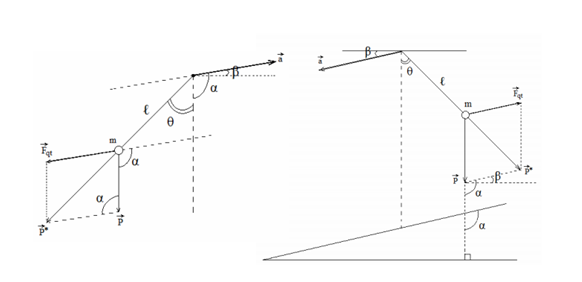
- Xiên xuống:
\(\begin{array}{l}P' = \sqrt {{P^2} + F_{qt}^2 - 2P.{F_{qt}}{\rm{cos}}\left( {{{90}^0} + \beta } \right)} \\ \to g' = \sqrt {{g^2} + {a^2} - 2g.ac{\rm{os(9}}{{\rm{0}}^0} + \beta )} \end{array}\)
Góc θ: \(\frac{a}{{\sin \theta }} = \frac{{g'}}{{\sin ({{90}^0} + \beta )}}\)
- Xiên lên:
\(\begin{array}{l}P' = \sqrt {{P^2} + F_{qt}^2 - 2P.{F_{qt}}{\rm{cos}}\left( {{{90}^0} - \beta } \right)} \\ \to g' = \sqrt {{g^2} + {a^2} - 2g.ac{\rm{os(9}}{{\rm{0}}^0} - \beta )} \end{array}\)
Vì \(cos(\pi - a) = - cosa\)
\( \to P' = \sqrt {{P^2} + F_{qt}^2 + 2P.{F_{qt}}{\rm{cos}}\alpha } \)
Góc θ: \(\frac{a}{{\sin \theta }} = \frac{{g'}}{{\sin ({{90}^0} - \beta )}}\)

