Con lắc đơn gồm một hòn bi có khối lượng m treo trên sợi dây dài ℓ = 1 m ở tại nơi có gia tốc trọng trường g = 9,8 m/s2. Bỏ qua mọi ma sát và lực cản môi trường. Con lắc trên được treo vào trần một ôtô chuyển động nhanh dần đều với gia tốc a = 2 m/s2 từ đỉnh mặt phẳng nghiêng với mặt phẳng ngang một góc 300. Hỏi con lắc dao động với chu kì bằng bao nhiêu ?
Trả lời bởi giáo viên
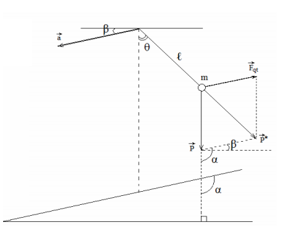
+ Oto lên nhanh dần xuống dốc nghiêng (\(\overrightarrow a \) xiên xuống) \( \to \overrightarrow {{F_{qt}}} \) xiên lên
Ta có:
\(\begin{array}{l}P' = \sqrt {{P^2} + F_{qt}^2 - 2P{F_{qt}}{\rm{cos(90 - }}\beta {\rm{)}}} \\ \to g' = \sqrt {{g^2} + {a^2} - 2g.a.c{\rm{os(90 - }}\beta {\rm{)}}} = \sqrt {{g^2} + {a^2} - 2g.a.c{\rm{os(90 - 3}}{{\rm{0}}^0}{\rm{)}}} = 8,969m/{s^2}\\ \to T' = 2\pi \sqrt {\frac{{\mathop{\rm l}\nolimits} }{{g'}}} = 2\pi \sqrt {\frac{1}{{8,969}}} = 2,098{\rm{s}}\end{array}\)
Hướng dẫn giải:
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực quán tính có phương xiên góc

