Một con lắc đơn dài \(l = {\rm{ }}25{\rm{ }}cm\), vật nặng có khối lượng \(m = 50g\) và mang điện tích \(q = - {10^{ - 4}}C\). Treo con lắc vào giữa hai bản kim loại thẳng đứng, song song, cách nhau \(d = 20cm\). Đặt vào hai bản hiệu điện thế một chiều \(U = 60V\). Lấy \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Chu kì dao động điều hoà của con lắc là:
Trả lời bởi giáo viên
Ta có:
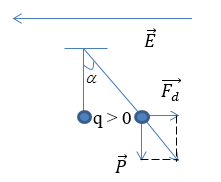
+ Hai bản kim loại thẳng đứng song song (là tụ phẳng) nên \(\overrightarrow E \) có phương ngang =>\(\overrightarrow {{F_d}} \) có phương ngang
+ Chu kì dao động của con lắc khi được tích điện q đặt giữa 2 bản kim loại là T’: \(T' = 2\pi \sqrt {\frac{l}{{g'}}} \)
Ta có:
\(\begin{array}{l}a = \frac{{{F_d}}}{m} = \frac{{\left| q \right|E}}{m} = \frac{{\left| q \right|\frac{U}{d}}}{m} = \frac{{\left| { - {{10}^{ - 4}}} \right|\frac{{60}}{{{{20.10}^{ - 2}}}}}}{{{{50.10}^{ - 3}}}} = 0,6m/{s^2}\\g' = \sqrt {{g^2} + {a^2}} \\ \to T' = 2\pi \sqrt {\frac{l}{{g'}}} = 2\pi \sqrt {\frac{l}{{\sqrt {{g^2} + {a^2}} }}} = 2\pi \sqrt {\frac{{0,25}}{{\sqrt {{{10}^2} + 0,{6^2}} }}} = 0,993{\rm{s}}\end{array}\)
Hướng dẫn giải:
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực điện
+ Áp dụng mối liên hệ giữa hiệu điện thế giữa hai bản tụ và cường độ điện trường: U = E.d

