Con lắc đơn trong phòng thí nghiệm có T=2s được treo vào trần một ô tô. Cho g=π2m/s2 . Biết ôtô lên dốc nhanh dần đều với gia tốc a=√3g. Biết dốc nghiêng một góc β=300 so với phương ngang. Hãy xác định vị trí cân bằng của con lắc và chu kì dao động nhỏ của nó ?
Trả lời bởi giáo viên
Ta có:
+ Chu kì dao động của con lắc đơn khi ở trong phòng thí nghiệm: T=2π√lg
+ Oto lên nhanh dần trên dốc nghiêng (→a xiên lên) →→Fqt xiên xuống
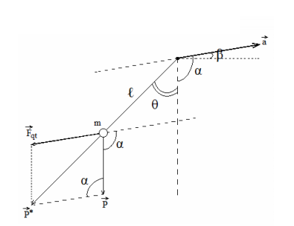
Ta có:
P′=√P2+F2qt−2PFqtcos(90+β)→g′=√g2+a2−2g.a.cos(90+β)=√g2+a2−2g.a.cos(90+300)=2,394gT′T=√gg′=√g2,394g=0,646→T′=0,646.2=1,293s
Góc θ:
asinθ=g′sin(900+β)→sinθ=asin(900+β)g′=√3g.sin(900+30)2,394g=0,627→α=38049′44
Hướng dẫn giải:
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: T=2π√lg
+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực quán tính có phương xiên góc

