Bài viết trình bày phương pháp giải các dạng bài tìm thời gian nén - giãn của CLLX: nằm ngang, treo thẳng đứng, nằm nghiêng.
DẠNG BÀI: TÍNH THỜI GIAN LÒ XO NÉN HAY GIÃN TRONG MỘT CHU KÌ.
Phương pháp:
1. Con lắc lò xo nằm ngang:
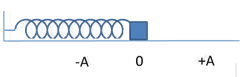
Thời gian lò xo giãn bằng thời gian lò xo nén
2. Con lắc lò xo treo thẳng đứng:
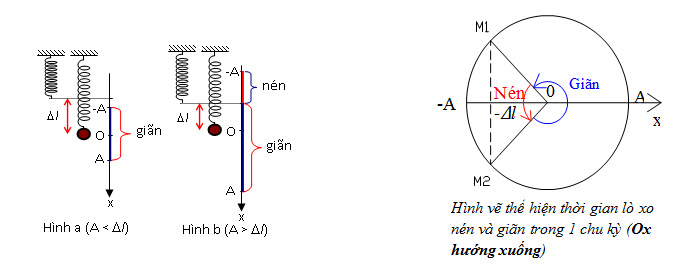
+ Khi \(A < \Delta {l_0}\) : Trong quá trình dao động, lò xo chỉ bị giãn mà không có nén => Thời gian lò xo giãn = T, thời gian lò xo nén = 0
+ Khi \(A > \Delta {l_0}\) :
- Thời gian lò xo nén 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\) đến \({x_2} = - A\) là : \(\Delta t = 2\frac{\alpha }{\omega }\) trong đó: \({\rm{cos}}\alpha {\rm{ = }}\frac{{\Delta {l_0}}}{A}\)
- Thời gian lò xo giãn 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\)đến \({x_2} = - A\) là: \(T - \Delta t\)
Trong một dao động (một chu kỳ) lò xo nén 2 lần và giãn 2 lần
3. Con lắc lò xo nằm nghiêng:
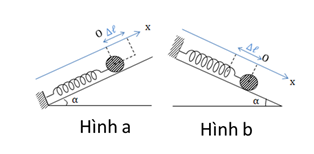
+ Khi \(A{\rm{ }} < \Delta {l_0}\) :
- Đầu cố định ở trên (Hình b): Trong quá trình dao động, lò xo chỉ bị giãn mà không có nén => Thời gian lò xo giãn = T, thời gian lò xo nén = 0
- Đầu cố định ở dưới (Hình a): Trong quá trình dao động, lò xo chỉ bị nén mà không có giãn => Thời gian lò xo giãn = 0, thời gian lò xo nén = T
+ Khi \(A{\rm{ }} > \Delta {l_0}\) :
- Thời gian lò xo nén 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\)đến \({x_2} = - A\)là : \(\Delta t = 2\frac{\alpha }{\omega }\) trong đó: \({\rm{cos}}\alpha {\rm{ = }}\frac{{\Delta {l_0}}}{A}\)
- Thời gian lò xo giãn 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\)đến \({x_2} = - A\)là: T-∆t
Trong một dao động (một chu kỳ) lò xo nén 2 lần và giãn 2 lần
