I- DẠNG 1: XÁC ĐỊNH THỜI GIAN NGẮN NHẤT VẬT ĐI TỪ A-B
Phương pháp
Vật có vận tốc lớn nhất khi qua VTCB, nhỏ nhất khi qua vị trí biên nên trong cùng một khoảng thời gian quãng đường đi được càng lớn khi vật ở càng gần VTCB và càng nhỏ khi càng gần vị trí biên.
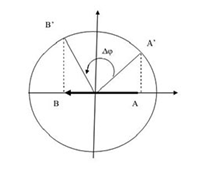
- Cách 1: Sử dụng đường tròn lượng giác
+ Bước 1: Xác định góc ∆φ
+ Bước 2: \(\Delta t = \frac{{\Delta \varphi }}{\omega } = \frac{{\Delta \varphi }}{{\frac{{2\pi }}{T}}} = \frac{{\Delta \varphi }}{{2\pi }}.T = \frac{{\Delta {\varphi ^0}}}{{360}}.T\)
Trong đó:
φ: góc theo rad
φ0: góc theo độ
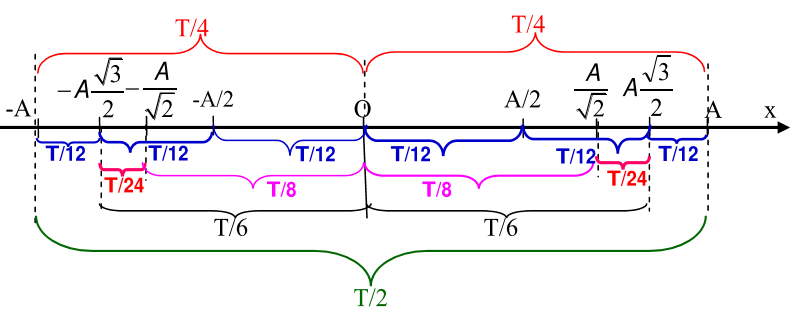
Cách 2: Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn.
II- DẠNG 2: XÁC ĐỊNH THỜI ĐIỂM VẬT ĐI QUA VỊ TRÍ ĐÃ BIẾT x (HOẶC v, A, WT, F) LẦN THỨ N.
Phương pháp
Trong 1 chu kì T vật đi qua x hai lần nếu không kể đến chiều chuyển động, nếu kể đến chiều chuyển động thì đi qua một lần.
- Qua x không kể đến chiều:
+ n chẵn: \(t = \frac{{n - 2}}{2}T + {t_2}\) với t2: thời gian để vật đi qua vị trí x lần thứ 2 kể từ thời điểm ban đầu.
+ n lẻ: \(t = \frac{{n - 1}}{2}T + {t_1}\) với t1: thời gian để vật đi qua vị trí x lần thứ 1 kể từ thời điểm ban đầu.
- Qua x kể đến chiều (theo chiều + hoặc -)
$t = (n - 1)T + {t_1}$ với t1 là thời gian để vật đi qua vị trí x theo chiều đầu bài yêu cầu lần thứ 1 kể từ thời điểm ban đầu.
Xác định t1, t2 như mục I
III- DẠNG 3: XÁC ĐỊNH SỐ LẦN VẬT ĐI QUA VỊ TRÍ ĐÃ BIẾT X (HOẶC V, A, WT, F) TỪ THỜI ĐIỂM T1 ĐẾN T2
- Cách 1: Phương pháp đại số
+ Giải phương trình lượng giác được các nghiệm
+ Từ t1 < t ≤ t2 Þ Phạm vi giá trị của (Với k Î Z)
+ Tổng số giá trị của k chính là số lần vật đi qua vị trí đó.
- Cách 2: Phương pháp ứng dụng vòng tròn lượng giác
+ Bước 1: Xác định T
+ Bước 2: tách \(\Delta t = aT + {t^*}\)
+ Bước 3: Xác định số lần vật qua vị trí x trong khoảng thời gian t* (n*)
=> Số lần vật qua vị trí x:
++ n= 2a + n* (nếu không kể đến chiều chuyển động)
++ n= a+n* (nếu qua vị trí biên hoặc khi kể đến chiều chuyển động)
Trong mỗi chu kỳ (mỗi dao động) vật qua mỗi vị trí biên 1 lần còn các vị trí khác 2 lần ( nếu không kể đến chiều chuyển động) và 1 lần (nếu kể đến chiều chuyển động).

