I. Bảng ghi nhớ các bước viết phương trình dao động sóng

II. Phương pháp giải bài tập sóng cơ - Phương trình sóng cơ
1. DẠNG 1: XÁC ĐỊNH BIÊN ĐỘ, LI ĐỘ, VẬN TỐC DAO ĐỘNG SÓNG CƠ:
Phương pháp:
- Cách 1: Thay vào phương trình sóng
\(\begin{array}{l}{u_M} = Ac{\rm{os}}\omega \left( {t - \dfrac{x}{v}} \right) = Ac{\rm{os}}\left( {\omega t - \dfrac{{2\pi x}}{\lambda }} \right)\\v = x' = - A\omega \sin \left( {\omega t - \dfrac{{2\pi x}}{\lambda }} \right)\end{array}\)
- Cách 2: Dùng vòng tròn lượng giác.
DĐĐH được xem là hình chiếu của một chất điểm chuyển động tròn đều lên một trục nằm trong mặt phẳng quỹ đạo. Với: \(A = R;\omega = \dfrac{v}{R}\)
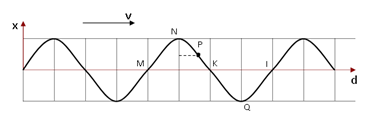
(VD: điểm N) xác định trạng thái dao động của điểm khác ta tiến hành như sau:
Nếu điểm đó sau N ( theo phương truyền sóng), ví dụ là điểm K, khi đó K sẽ trễ pha hơn N góc \(\Delta \varphi = 2\pi \dfrac{{\Delta d}}{\lambda }\) với \(\Delta d = {\rm{ }}NK\). Từ N quay góc \(\Delta \phi \) theo chiều kim đồng hồ ta sẽ xác định được trạng thái của K.
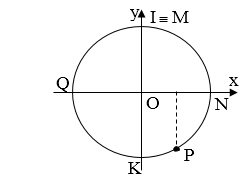
Nếu điểm cần tìm trước N (theo phương truyền sóng), ví dụ là M, ta cũng tính \(\Delta \varphi \) theo công thức trên với \(\Delta d = MN\) , từ N quay theo chiểu ngược kim đồng hồ góc \(\Delta \varphi \) ta được M
2. DẠNG 2: VIẾT PHƯƠNG TRÌNH DAO ĐỘNG TẠI MỘT ĐIỂM TRÊN PHƯƠNG TRUYỀN SÓNG
Phương pháp:
Phương trình tại nguồn: \({u_0} = Ac{\rm{os}}\omega {\rm{t}}\)
PT sóng có dạng: \({u_M} = Ac{\rm{os}}\omega \left( {t - \dfrac{x}{v}} \right) = Ac{\rm{os}}\left( {\omega t - \dfrac{{2\pi x}}{\lambda }} \right)\)
- Bước 1: Xác định A, ω, φ: dựa theo dữ kiện đề bài cho.
pha ban đầu của sóng tại M: \({\varphi _M} = \varphi - 2\pi \dfrac{{\overline {OM} }}{\lambda } = \varphi - 2\pi \dfrac{x}{\lambda }\)
- Bước 2: Viết phương trình sóng
- Nếu M ở trước O theo chiều truyền sóng thì \({\varphi _M} = \varphi + {\rm{ }}2\pi \dfrac{x}{\lambda }\); M ở sau O theo chiều truyền sóng thì \({\varphi _M} = \varphi - {\rm{ }}2\pi \dfrac{x}{\lambda }\).
- Hàm cos và hàm sin là hàm tuần hoàn với chu kì \(2\pi \) nên trong pha ban đầu của phương trình sóng ta có thể cộng vào hoặc trừ đi một số chẵn của \(\pi \)để pha ban đầu trong phương trình có trị tuyệt đối nhỏ hơn \(2\pi \).

