Một vật dao động điều hòa quanh vị trí cân bằng O. Tại thời điểm ban đầu vật đang ở vị trí biên. Sau đó \(\dfrac{1}{3}\,\,s\) vật không đổi chiều chuyển động và tới vị trí có tốc độ bằng một nửa tốc độ cực đại. Sau đó vật chuyển động thêm \(\dfrac{4}{3}\,\,s\) và đi được quãng đường dài 9 cm. Tốc độ dao động cực đại của vật là

Tại vị trí vật có tốc độ bằng một nửa tốc độ cực đại, ta có công thức độc lập với thời gian:

\(\dfrac{{{x^2}}}{{{A^2}}} + \dfrac{{{v^2}}}{{{v_{\max }}^2}} = 1 \Rightarrow \dfrac{{{x^2}}}{{{A^2}}} + {\left( {\dfrac{1}{2}} \right)^2} = 1 \Rightarrow x =  \pm \dfrac{{A\sqrt 3 }}{2}\)

Ta có vòng tròn lượng giác:

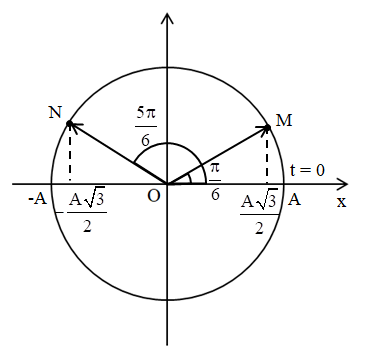
Trường hợp 1: ở thời điểm \(t = \dfrac{1}{3}\,\,s\), vecto quay ở vị trí M, ta có:

\(\Delta \varphi  = \omega \Delta t \Rightarrow \dfrac{\pi }{6} = \omega .\dfrac{1}{3} \Rightarrow \omega  = \dfrac{\pi }{2}\,\,\left( {rad/s} \right)\)

Vật chuyển động thêm \(\dfrac{4}{3}\,\,s\), vecto quay được góc là:

\(\Delta \varphi ' = \omega \Delta t' = \dfrac{\pi }{2}.\dfrac{4}{3} = \dfrac{{2\pi }}{3}\,\,\left( {rad} \right)\)

→ vecto quay tới vị trí N

Quãng đường vật đi được là:

\(\begin{array}{l}2.\dfrac{{A\sqrt 3 }}{2} = 9\,\,\left( {cm} \right) \Rightarrow A = 3\sqrt 3 \,\,\left( {cm} \right)\\ \Rightarrow {v_{\max }} = \omega A = \dfrac{\pi }{2}.3\sqrt 3  \approx 8,16\,\,\left( {cm/s} \right)\end{array}\)

Trường hợp 2: ở thời điểm \(\dfrac{1}{3}\,\,s\), vecto quay ở vị trí N, ta có:

\(\Delta \varphi  = \omega \Delta t \Rightarrow \dfrac{{5\pi }}{6} = \omega .\dfrac{1}{3} \Rightarrow \omega  = \dfrac{{5\pi }}{2}\,\,\left( {rad/s} \right)\)

Vật chuyển động thêm \(\dfrac{4}{3}\,\,s\), vecto quay được góc là:

\(\Delta \varphi ' = \omega \Delta t' = \dfrac{{5\pi }}{2}.\dfrac{4}{3} = \dfrac{{10\pi }}{3}\,\,\left( {rad} \right) = 2\pi  + \dfrac{{4\pi }}{3}\)

→ vecto quay được 1 vòng và tới vị trí N

Quãng đường vật đi được là:

\(\begin{array}{l}4A + 2A + 2.\left( {A - \dfrac{{A\sqrt 3 }}{2}} \right) = 9\,\,\left( {cm} \right)\\ \Rightarrow A = \dfrac{9}{{8 - \sqrt 3 }} \approx 1,436\,\,\left( {cm} \right)\\ \Rightarrow {v_{\max }} = \omega A = \dfrac{{5\pi }}{2}.1,436 \approx 11,28\,\,\left( {cm/s} \right)\end{array}\)