Câu hỏi:
2 năm trước
Một chất điểm dao động điều hòa với chu kì $T$. Trong khoảng thời gian ngắn nhất khi đi từ vị trí biên có li độ $x = A$ đến vị trí $x = - \dfrac{A}{2}$, chất điểm có tốc độ trung bình là:
Một chất điểm dao động điều hòa với chu kì $T$. Trong khoảng thời gian ngắn nhất khi đi từ vị trí biên có li độ $x = A$ đến vị trí $x = - \dfrac{A}{2}$, chất điểm có tốc độ trung bình là:
Trả lời bởi giáo viên
Đáp án đúng: b
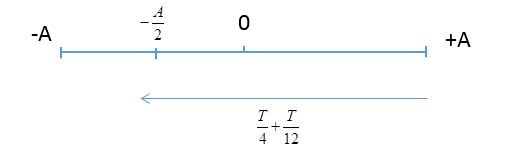
Khoảng thời gian ngắn nhất khi đi từ vị trí $A$ đến $- A/2$ là: \(\Delta t = \dfrac{T}{4} + \dfrac{T}{{12}} = \dfrac{T}{3}\)
Quãng đường đi được khi đi từ vị trí $A$ đến $- A/2$ là: \(S = \dfrac{{3A}}{2}\)
=> Tốc độ trung bình của chất điểm khi đi từ vị trí $A$ đến $- A/2$ là: \({v_{TB}} = \dfrac{S}{{\Delta t}} = \dfrac{{\dfrac{{3A}}{2}}}{{\dfrac{T}{3}}} = \dfrac{{9A}}{{2T}}\)
Hướng dẫn giải:
+ Sử dụng trục thời gian suy ra từ vòng tròn
+ Áp dụng biểu thức xác định tốc độ trung bình của vật: \({v_{TB}} = \dfrac{S}{{\Delta t}}\)

