Câu hỏi:
2 năm trước
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự $A, M, N$ và $B$. Giữa hai điểm $A$ và $M$ chỉ có điện trở thuần, giữa hai điểm $M$ và $N$ chỉ có tụ điện, giữa hai điểm $N$ và $B$ có cuộn cảm. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều $240V - 50Hz$ thì $u_{MB}$ và $u_{AM}$ lệch pha nhau \(\dfrac{\pi }{3}\), $u_{AB}$ và $u_{AM}$ lệch pha nhau \(\dfrac{\pi }{6}\) . Điện áp hiệu dụng trên $R$ là:
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có: $u_{MB}$ và $u_{AM}$ lệch pha nhau \(\dfrac{\pi }{3}\)
=> cuộn cảm không thuần cảm, có điện trở trong $r$
Vẽ lại mạch điện và vẽ giản đồ véc tơ, ta có:
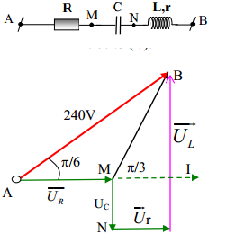
$\angle BAM = \dfrac{\pi }{6};\angle AMB = \pi - \angle BMI = \pi - \dfrac{\pi }{3} = \dfrac{{2\pi }}{3} \to \angle ABM = \pi - \left( {\angle BAM + \angle AMB} \right) = \dfrac{\pi }{6}$
$\dfrac{{{U_R}}}{{\sin \angle ABM}} = \dfrac{{{U_{AB}}}}{{\sin \angle AMB}} \leftrightarrow \dfrac{{{U_R}}}{{\sin \dfrac{\pi }{6}}} = \dfrac{{{U_{AB}}}}{{\sin \dfrac{{2\pi }}{3}}} \to {U_R} = \dfrac{{{U_{AB}}}}{{\sin \dfrac{{2\pi }}{3}}}\sin \dfrac{\pi }{6} = \dfrac{{240}}{{\dfrac{{\sqrt 3 }}{2}}}\dfrac{1}{2} = \dfrac{{240}}{{\sqrt 3 }} = 80\sqrt 3 V$
Hướng dẫn giải:
+ Sử dụng giản đồ véctơ
+ Sử dụng định lí hàm số sin:
\(\dfrac{a}{{{\mathop{\rm sinA}\nolimits} }} = \dfrac{b}{{{\mathop{\rm sinB}\nolimits} }} = \dfrac{c}{{{\mathop{\rm sinC}\nolimits} }}\)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
