Đặt điện áp \(u = U\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{6}} \right)V\) vào hai đầu đoạn mạch AB. Đoạn AB có 4 điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có điện trở thuần R, giữa hai điểm M và N chỉ có cuộn dây có cảm kháng 100Ω có điện trở r = 0,5R, giữa 2 điểm N và B chỉ có tụ điện có dung kháng 200Ω. Điện áp hiệu dụng trên đoạn AN là 200V. Điện áp tức thời trên đoạn MN và AB lệch pha nhau \(\dfrac{\pi }{2}\). Nếu biểu thức dòng điện trong mạch là \(i = I\sqrt 2 {\rm{cos}}\left( {100\pi t + {\varphi _i}} \right)A\) thì giá trị của I và \({\varphi _i}\) lần lượt là:
Trả lời bởi giáo viên
Vẽ lại mạch điện và giản đồ véctơ, ta được:
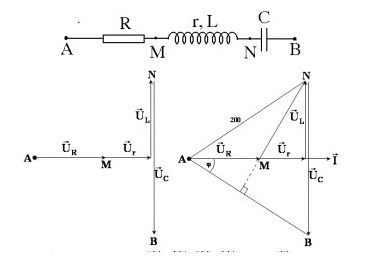
Từ giản đồ, ta có: M vừa là trọng tâm vừa là trực tâm => Tam giác AMB là tam giác đều
=> UC = UAN = 200V
\(I = \frac{{{U_C}}}{{{Z_C}}} = 1A\)
và i sớm pha hơn uAB một góc \(\dfrac{\pi }{6}\)
\( \to i = \sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{6} + \dfrac{\pi }{6}} \right) = \sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{3}} \right)A\)
Hướng dẫn giải:
Sử dụng giản đồ véctơ

