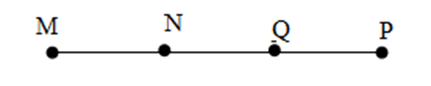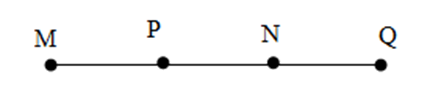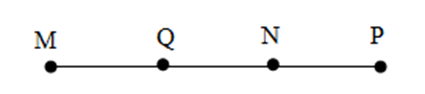Cho hình vẽ sau
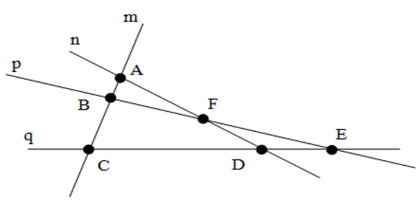
Trên hình vẽ có bao nhiêu điểm chỉ thuộc hai đường thẳng?
Tất cả các đường thẳng đi qua:
+ Điểm \(A:\) \(m,n\) nên có \(2\) đường thẳng qua \(A\)
+ Điểm \(B:\) \(m,p\) nên có \(2\) đường thẳng qua \(B\)
+ Điểm \(C:\) \(m,q\) nên có \(2\) đường thẳng qua \(C\)
+ Điểm \(D:\) \(n,q\) nên có \(2\) đường thẳng qua \(D\)
+ Điểm \(E:\) \(p,q\) nên có \(2\) đường thẳng qua \(E\)
+ Điểm \(F:\) \(n,p\) nên có \(2\) đường thẳng qua \(F\)
Vậy tất cả \(6\) điểm \(A,B,C,D,E,F\) đều chỉ thuộc hai đường thẳng.
Cho hình vẽ sau

Trên hình vẽ, có bao nhiêu đường thẳng đi qua ba điểm?
Trên hình vẽ, các điểm thuộc đường thẳng:
+ \(m\) là \(A,B,C\) nên có \(3\) điểm thuộc \(m\)
+ \(n\) là \(A,F,D\) nên có \(3\) điểm thuộc \(n\)
+ \(p\) là \(B,F,E\) nên có \(3\) điểm thuộc \(p\)
+ \(q\) là \(C,D,E\) nên có \(3\) điểm thuộc \(q\)
Vậy có tất cả \(4\) đường thẳng mà mỗi đường thẳng đi qua \(3\) điểm trong hình.
Có bao nhiêu bộ ba điểm thẳng hàng trong hình vẽ dưới đây?
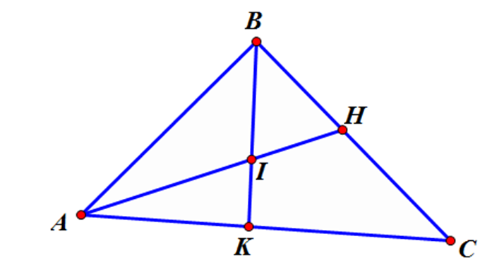
Các bộ ba điểm thẳng hàng trong hình vẽ là:
\(\left( {A,I,H} \right),\left( {B,I,K} \right),\) \(\left( {A,K,C} \right),\left( {B,H,C} \right).\)
Vậy có \(4\) cặp điểm thỏa mãn bài toán.
Có bao nhiêu bộ ba điểm không thẳng hàng trong hình vẽ sau
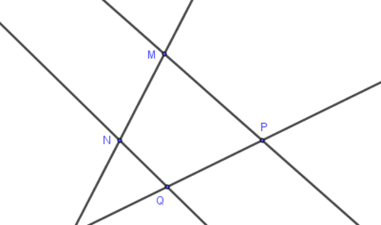
Các bộ ba điểm trong hình vẽ là:
\(\left( {M,N,P} \right),\left( {M,N,Q} \right),\) \(\left( {M,P,Q} \right),\left( {N,P,Q} \right)\)
Vậy có \(4\) bộ ba điểm không thẳng hàng.
Cho bốn điểm $M;N;P;Q$ cùng nằm trên một đường thẳng và hai điểm $M;N$ nằm cùng phía đối với điểm $Q$ còn hai điểm $N,P$ nằm khác phía đối với điểm $Q.$ Một hình vẽ đúng là:
Đáp án A: Hai điểm \(M,N\) nằm cùng phía so với \(Q\) và hai điểm \(N,P\) khác phía so với \(Q\) nên thỏa mãn, chọn A.
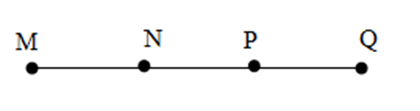
Đáp án B: Hai điểm \(N,P\) cùng phía so với \(Q\) nên không thỏa mãn, loại B.
Đáp án C: Hai điểm \(N,P\) cùng phía so với \(Q\) nên không thỏa mãn, loại C.
Đáp án D: Hai điểm \(M,N\) nằm khác phía so với \(Q\) nên không thỏa mãn, loại D.
Cho $5$ điểm $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}O$ sao cho $3$ điểm $A,{\rm{ }}B,{\rm{ }}C$ cùng thuộc đường thẳng $d;$ $3$ điểm $B,{\rm{ }}C,{\rm{ }}D$ thẳng hàng và $3$ điểm $C,{\rm{ }}D,{\rm{ }}O$ không thẳng hàng. Hỏi điểm nào nằm ngoài đường thẳng $d?$
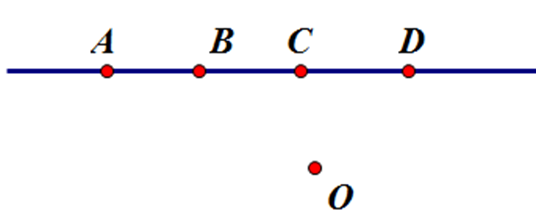
Vì ba điểm \(A,B,C\) thuộc \(d\) và \(B,C,D\) thẳng hàng nên \(D \in d\)
Mà \(C,D \in d\) nên nếu \(C,D,O\) không thẳng hàng thì \(O \notin d\)
Vậy điểm \(O\) không thuộc đường thẳng \(d\)
Cho hình vẽ sau:
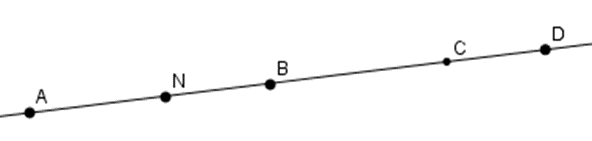
Kể tên các điểm nằm giữa \(A\) và \(D.\)
Các điểm nằm giữa \(A\) và \(D\) là \(N,B,C\)
Cho hình vẽ sau:

Có bao nhiêu điểm nằm giữa \(N\) và \(D?\)
Các điểm nằm giữa \(N\) và \(D\) là \(B,C\)
Vậy có \(2\) điểm cần tìm.
Cho hình vẽ sau:

Số cặp điểm nằm cùng phía với điểm \(A\) là:
Các cặp điểm nằm cùng phía so với điểm \(A\) là:
\(\left( {N,B} \right),\left( {N,C} \right),\left( {N,D} \right),\) \(\left( {B,C} \right),\left( {B,D} \right),\left( {C,D} \right)\)
Vậy có \(6\) cặp điểm thỏa mãn bài toán.
Cho hình vẽ sau:

Trên hình vẽ, điểm \(B\) nằm giữa bao nhiêu cặp điểm?
Điểm \(B\) nằm giữa các cặp điểm là:
\(\left( {N,C} \right),\left( {A,D} \right),\left( {A,C} \right),\left( {N,D} \right)\)
Vậy có \(4\) cặp điểm thỏa mãn bài toán.
Cho hình vẽ sau:

Trên hình vẽ, điểm \(B\) và \(D\) nằm khác phía với mấy điểm?
Trong hình vẽ chỉ có điểm \(C\) nằm giữa hai điểm \(B\) và \(D\) nên chỉ có \(1\) điểm thỏa mãn yêu cầu bài toán.
Cho hình vẽ sau:

Trên hình vẽ, điểm \(A\) và \(B\) nằm cùng phía với các điểm nào?
Trên hình vẽ, hai điểm \(A,B\) nằm cùng phía so với các điểm \(C,D\).
Cho hình vẽ sau:

Điểm \(A\) và \(C\) nằm cùng phía với điểm nào?
Trên hình vẽ, hai điểm \(A,C\) nằm cùng phía so với điểm \(D\) và nằm khác phía so với điểm \(B\).
Cho hình vẽ sau:

Chọn câu sai.
Đáp án A: Điểm \(B\) nằm giữa \(A\) và \(C\) nên A đúng và C sai.
Đáp án B: Điểm \(B\) nằm giữa \(A\) và \(D\) nên B đúng.
Điểm \(C\) nằm giữa \(D\) và \(A\) nên D đúng.