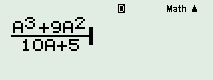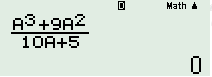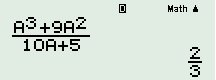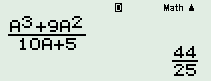Bài tập cuối chương I

+) $M = \left\{ {0;\,2;\,4;\,6;\,8;\,10 ;\,12;...} \right\};$ $N = \left\{ {0;\,6;\,12;...} \right\}$

Ta thấy các phần tử của $N$ đều xuất hiện trong tập $M$ nên $N$ là tập con của $M$ 

$\Rightarrow N \subset M \Rightarrow M \cap N = N$ $\Rightarrow$A sai và C đúng

+) $P = \left\{ {1;\,2} \right\};$ $Q = \left\{ {1;\,2;\,3;\,6} \right\}$ $\Rightarrow \,\,P \subset Q,\,\,P \cap Q = P$

$\Rightarrow$ B và D đều sai.

$A = \left\{ {0;1;2;3;4} \right\},B = \left\{ {2;3;4;5;6} \right\}.$

$A\backslash B = \left\{ {0;1} \right\},\,\,B\backslash A = \left\{ {5;6} \right\}$$\Rightarrow \left( {A\backslash B} \right) \cup \left( {B\backslash A} \right) = \left\{ {0;1;5;6} \right\}$

${C_\mathbb{R}}A = \left[ { - 3;\sqrt 8 } \right)$, ${C_\mathbb{R}}B = \left( { - 5;2} \right) \cup \left( {\sqrt 3 ;\sqrt {11} } \right) = \left( { - 5;\,\sqrt {11} } \right)$

$A = \left( { - \infty ;\, - 3} \right) \cup \left[ {\sqrt 8 ; + \infty } \right)$, $B = \left( { - \infty ; - 5} \right] \cup \left[ {\sqrt {11} ; + \infty } \right).$

$\Rightarrow A \cap B = \left( { - \infty ; - 5} \right] \cup \left[ {\sqrt {11} ; + \infty } \right)$$\Rightarrow {C_\mathbb{R}}\left( {A \cap B} \right) = \left( { - 5;\sqrt {11} } \right).$

$\left( { - \infty ;9a} \right) \cap \left( {\dfrac{4}{a}; + \infty } \right) \ne \emptyset \,\,\left( {a < 0} \right)$ $\Leftrightarrow \,\,\dfrac{4}{a} < 9a\,$ $\Leftrightarrow \,\,\dfrac{4}{a} - 9a\,\, < 0\,$

$\Leftrightarrow \dfrac{{4 - 9{a^2}}}{a} < 0$$\Leftrightarrow \left\{ \begin{array}{l}4 - 9{a^2} > 0\\a < 0\,\,\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l} - \dfrac{2}{3} < a < \dfrac{2}{3}\\a < 0\end{array} \right.$

$\Leftrightarrow  - \dfrac{2}{3} < a < 0$.

Bước 1:

Ta có $A = \left\{ {x \in R:x + 2 \ge 0} \right\}$$\Rightarrow A = \left[ { - 2;\, + \infty } \right)$,

$B = \left\{ {x \in R:5 - x \ge 0} \right\}$$\Rightarrow B = \left( { - \infty ;\,5} \right]$.

Bước 2:

Biểu diễn trên trục số: 

Ta gạch bỏ phần không thuộc tập hợp A (Màu xanh) và phần thuộc tập hợp B (Màu cam) thì được hiệu (phần không bị gạch):

$\Rightarrow A\backslash B = \left( {5;\, + \infty } \right).$

+ Do $A,B \ne \emptyset$ ta có điều kiện $\left\{ \begin{array}{l}m - 1 < 4\\2m + 2 >  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 5\\m >  - 2\end{array} \right.$ $\Leftrightarrow  - 2 < m < 5$

Để $A \cap B = \emptyset  \Leftrightarrow 2m + 2 \le m - 1 \Leftrightarrow m \le  - 3$ (không thỏa điều kiện $- 2 < m < 5$)

Do đó không có giá trị nào của $m$ để $A \cap B = \emptyset$

Vậy với mọi $m \in \left( { - 2;5} \right)$ thì $A \cap B \ne \emptyset$

Đáp án B sai vì học sinh không tìm điều kiện.

Đáp án C sai vì học sinh giải sai $m - 1 >  - 2 \Leftrightarrow m >  - 1$ và kết hợp với điều kiện.

Đáp án D sai vì học sinh giải sai $4 < 2m + 2 \Leftrightarrow m > 1$. Kết hợp với điều kiện

Với $2$ tập khác rỗng $A,B$ ta có điều kiện $\left\{ \begin{array}{l}m - 1 < 4\\2m + 2 >  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 5\\m >  - 2\end{array} \right.$ $\Leftrightarrow  - 2 < m < 5$

Để $A \subset B \Leftrightarrow \left\{ \begin{array}{l}m - 1 \ge  - 2\\2m + 2 > 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge  - 1\\2m + 2 > 4\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}m \ge  - 1\\m > 1\end{array} \right. \Leftrightarrow m > 1$

So với điều kiện $1 < m < 5$

Đáp án B sai vì học sinh không giải điều kiện.

Đáp án C sai vì học sinh giải:

Với $2$ tập khác rỗng $A, B$ ta có điều kiện $\left\{ \begin{array}{l}m - 1 < 4\\2m + 2 >  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 5\\m >  - 2\end{array} \right.$ $\Leftrightarrow  - 2 < m < 5$

Để $A \subset B \Leftrightarrow m - 1 \ge  - 2 \Leftrightarrow m \ge  - 1$. Kết hợp với điều kiện được kết quả $- 1 \le m < 5$

Đáp án D sai vì học sinh giải $A \subset B \Leftrightarrow \left\{ \begin{array}{l}m - 1 <  - 2\\2m + 2 < 4\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}m <  - 1\\m < 1\end{array} \right. \Leftrightarrow m <  - 1$

Kết hợp với điều kiện $- 2 < m <  - 1$

Điều kiện $a \le 8 - a \Leftrightarrow a \le 4$.

Khi đó để tập $A$ có độ dài là $5$ thì $8 - a - a = 5 \Leftrightarrow a = \dfrac{3}{2}$(thỏa điều kiện).

Đáp án B sai vì học sinh giải $a - \left( {8 - a} \right) = 5 \Leftrightarrow a = \dfrac{{13}}{2}$

Đáp án C sai vì học sinh giải $8 - a = 5 \Leftrightarrow a = 3$.

Đáp án D sai vì học sinh chỉ giải $a < 8 - a \Leftrightarrow a < 4$.

*) Vì $a \in \mathbb{N},\,\,a \le 2 \Rightarrow a \in \left\{ {0;\,\,1;\,\,2} \right\}$.

*) Nhập biểu thức của $x$ vào máy tính.

*) Thay lần lượt giá trị của $a$ vào biểu thức để tìm $x$.

Với $a = 0$: Nhấn phím “CALC” + “0” + “=” ta được: 

Với $a = 1$: Nhấn phím “CALC” + “1” + “=” ta được: 

Với $a = 2$: Nhấn phím “CALC” + “2” + “=” ta được: 

$\Rightarrow A = \left\{ {0;\,\,\dfrac{2}{3};\,\,\dfrac{{44}}{{25}}} \right\}$

*) $A = \left\{ {x \in \mathbb{Q}|{x^2} - 4x + 2 = 0} \right\}$

Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: ${x^2} - 4x + 2 = 0$

${x^2} - 4x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 2 \\x = 2 - \sqrt 2 \end{array} \right.$

Mà $x \in \mathbb{Q}$ nên $A = \emptyset$.

*) $B = \left\{ {x \in \mathbb{R}|{x^2} - x + 1 = 0} \right\}$                                                   

Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: ${x^2} - x + 1 = 0$.

$\Rightarrow B = \emptyset$                                              

*) $C = \left\{ {x \in \mathbb{N}|{x^2} + 7x + 12 = 0} \right\}$                                              

Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: ${x^2} + 7x + 12 = 0$.

${x^2} + 7x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 3\\x =  - 4\end{array} \right.$

Mà $x \in \mathbb{N} \Rightarrow C = \emptyset$.

*) $D = \left\{ {x \in \mathbb{R}|{x^2} - 4x + 2 = 0} \right\}$

Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: ${x^2} - 4x + 2 = 0$

${x^2} - 4x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 2 \\x = 2 - \sqrt 2 \end{array} \right.$

Mà $x \in \mathbb{R}$ nên $D = \left\{ {2 - \sqrt 2 ;\,\,2 + \sqrt 2 } \right\}$.

*) $A = \left\{ {\left. {x \in \mathbb{Z}} \right|\left( {{x^2} - 2} \right)\left( {{x^2} + 9} \right) = 0} \right\}$

$\left( {{x^2} - 2} \right)\left( {{x^2} + 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - 2 = 0\\{x^2} + 9 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 2 \\x =  - \sqrt 2 \end{array} \right.$

Mà $x \in \mathbb{Z}$ nên $A = \emptyset$.

*) Tập hợp B:

$B=\left\{ {x \in \mathbb{N}|\left( {x + 1} \right)\left( {x - 2} \right)\left( {{x^2} - 7x + 6} \right) = 0} \right\}$

Nhấn “MODE” + “5” + “1” để giải phương trình bậc hai: ${x^2} - 7x + 6 = 0$

$\left( {x + 1} \right)\left( {x - 2} \right)\left( {{x^2} - 7x + 6} \right) = 0$$\Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 2 = 0\\{x^2} - 7x + 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 2\\x = 6\\x = 1\end{array} \right.$

Mà $x \in \mathbb{N}$ nên $B = \left\{ {1;\,\,2\,;\,\,6} \right\}$.

Số phần tử của tập hợp $A$ và $B$ là: $0 + 3 = 3$ (phần tử).

TH1:

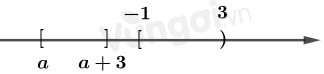
TH2:

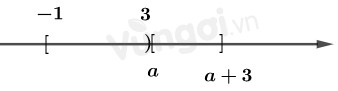
$A \cap B = \emptyset \Leftrightarrow \left[ \matrix{ a + 3 < - 1 \hfill \cr a \ge 3 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ a < - 4 \hfill \cr a \ge 3 \hfill \cr} \right.$

Ta có:  $A\backslash B = \left\{ {0;\,1} \right\}.$