Tìm giá trị nhỏ nhất của hàm số: \(y = \sqrt[3]{{{x^4} + 2{x^2} + 1}} - 3\sqrt[3]{{{x^2} + 1}} + 1\)
Đặt \(t = \sqrt[3]{{{x^2} + 1}},\,\,t \ge 1 \Rightarrow {t^2} = \sqrt[3]{{{x^4} + 2{x^2} + 1}}\)
Khi đó hàm số trở thành \(y = {t^2} - 3t + 1\) với \(t \ge 1\).
Bảng biến thiên
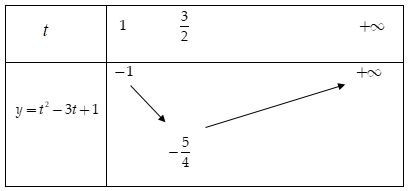
Suy ra giá trị nhỏ nhất của hàm số \(y = \sqrt[3]{{{x^4} + 2{x^2} + 1}} - 3\sqrt[3]{{{x^2} + 1}} + 1\) là \( - \dfrac{5}{4}\) khi và chỉ khi $t = \dfrac{3}{2}$ hay \(\sqrt[3]{{{x^2} + 1}} = \dfrac{3}{2} \Leftrightarrow x = \pm \sqrt {\dfrac{{19}}{8}} \)
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \({x^2} - 3x + 2 - m = 0\) có nghiệm trên đoạn \(\left[ { - 1;2} \right]\) ?
\({x^2} - 3x + 2 - m = 0 \Rightarrow m = {x^2} - 3x + 2\,\,\,\left( 1 \right)\)
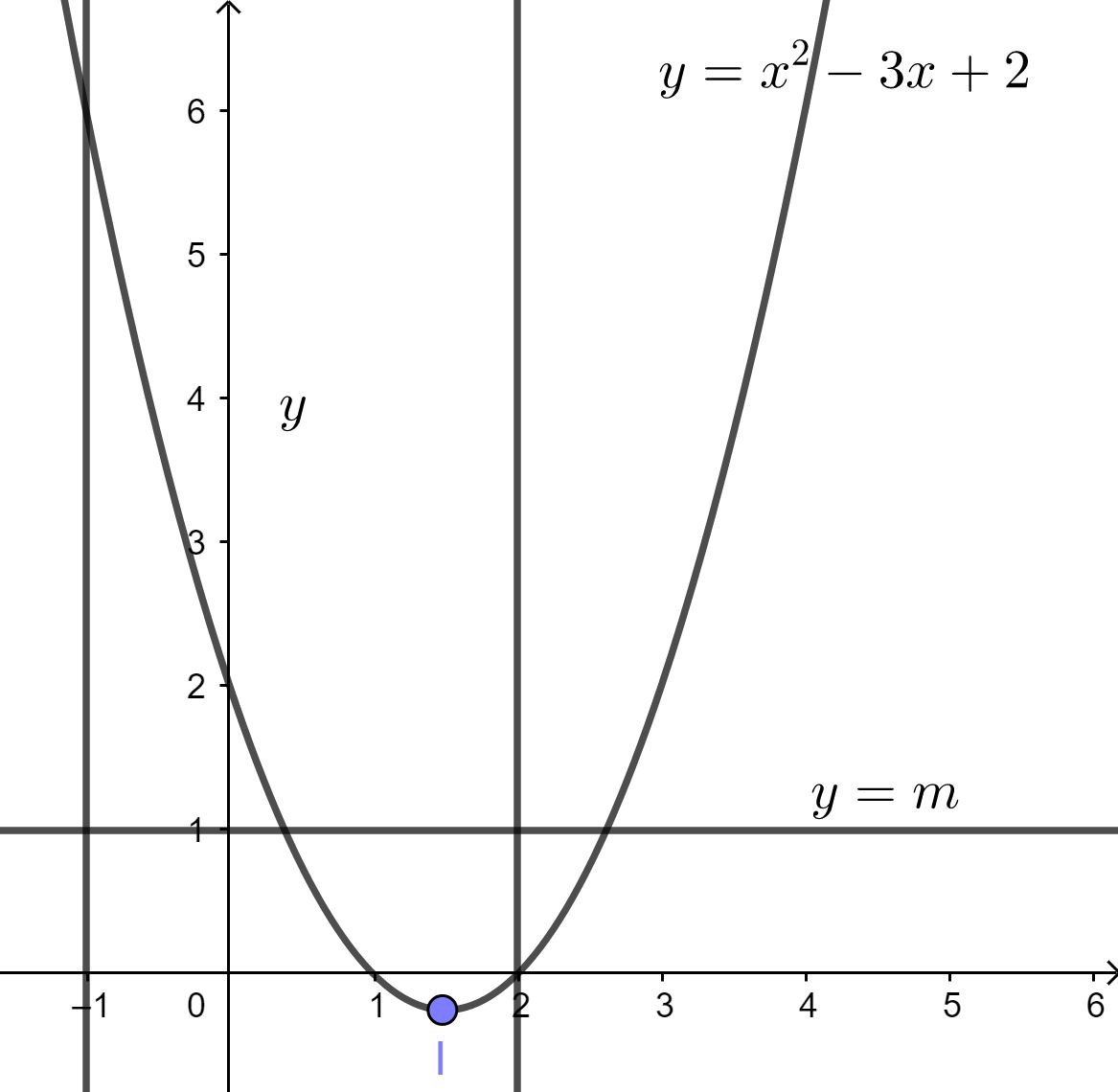
Số nghiệm của phương trình (1) trên \(\left[ { - 1;2} \right]\) là số giao điểm của đồ thị hàm số \(y = {x^2} - 3x + 2\) với đường thẳng \(y = m\) song song \(Ox\) trên \(\left[ { - 1;2} \right]\)
Đồ thị có đỉnh \(I\left( {\dfrac{3}{2};\dfrac{{ - 1}}{4}} \right)\)
\(f\left( { - 1} \right) = 6;f\left( 2 \right) = 0\)
Để phương trình (1) có nghiệm thì \(\dfrac{{ - 1}}{4} \le m \le 6\). Do \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1;2;3;4;5;6} \right\}\)
Tìm tất cả các giao điểm của parabola \(\left( P \right):y = 2{x^2} - x + 2\) với đường thẳng \(d:y = 3\).
Xét phương trình hoành độ giao điểm ta có: \(2{x^2} - x + 2 = 3 \Leftrightarrow 2{x^2} - x - 1 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{{ - 1}}{2}\end{array} \right.\)
Vậy tọa độ giao điểm là \(\left( {1;3} \right),\left( { - \dfrac{1}{2};3} \right)\)

