I. Ứng dụng trong giải bài toán Hóa học, Vật lý, Sinh học
Ví dụ 1: Cân bằng phương trình phản ứng hoá học khi đốt cháy nhôm trong oxygen:
\({\rm{Al}} + {{\rm{O}}_2}\mathop \to \limits^{{t^o}} {\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}\)
Giải
Giả sử x, y, z là ba số nguyên dương thoả mãn cân bằng phương trình phản ứng hoá học:
\({\rm{x}}\,{\rm{Al}} + y\,{{\rm{O}}_2}\mathop \to \limits^{{t^o}} {\rm{z A}}{{\rm{l}}_2}{{\rm{O}}_3}\)
Số nguyên tử nhôm ở hai vế bằng nhau, ta có \(x = 2z\).
Số nguyên tử oxygen ở hai vế bằng nhau, ta có \(2y = 3z\).
Từ đó, ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x = 2z}\\{2y = 3z}\end{array}} \right.\).
Vì \(y\) là số nguyên dương nên ta chọn \(z = 2n\), với \(n\) là số nguyên dương.
Hệ phương trình có vô số nghiệm dạng \((4n;3n;2n)\), trong đó \(n\) là số nguyên dương.
Để phương trình có hệ số đơn giản, ta chọn \(n = 1\), ta có \(x = 4,y = 3\) và \(z = 2\).
Vậy phương trình cân bằng phản ứng hoá học là \(4\,{\rm{Al}} + 3\,{{\rm{O}}_2}\mathop \to \limits^{{t^o}} {\rm{2 A}}{{\rm{l}}_2}{{\rm{O}}_3}\).
Ví dụ 2: Cho một đoạn mạch điện như Hình 1 .
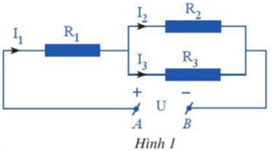
Biết \({{\rm{R}}_1} = 36\Omega ,{{\rm{R}}_2} = 90\Omega ,{{\rm{R}}_3} = 60\Omega \) và \({\rm{U}} = 60\;{\rm{V}}\). Gọi \({{\rm{I}}_1}\) là cường độ dòng điện của mạch chính, \({{\rm{I}}_2}\) và \({{\rm{I}}_3}\) là cường độ dòng điện của hai nhánh. Tính \({{\rm{I}}_1},{{\rm{I}}_2},{{\rm{I}}_3}\).
Giải
Cường độ dòng điện của đoạn mạch mắc song song là: \({{\rm{I}}_2} + {{\rm{I}}_3}\).
Ta có: \({{\rm{I}}_1} = {{\rm{I}}_2} + {{\rm{I}}_3}\) hay \({{\rm{I}}_1} - {{\rm{I}}_2} - {{\rm{I}}_3} = 0\).
Hiệu điện thế ở đoạn mạch mắc song song là: \({{\rm{U}}_2} = {{\rm{R}}_2} \cdot {{\rm{I}}_2} = {{\rm{R}}_3} \cdot {{\rm{I}}_3}\) nên \(90{{\rm{I}}_2} = 60{{\rm{I}}_3}\) hay \(3{{\rm{I}}_2} - 2{{\rm{I}}_3} = 0\).
Hiệu điện thế của đoạn mạch là: \({\rm{U}} = {{\rm{U}}_1} + {{\rm{U}}_2}\) nên \(60 = {{\rm{R}}_1}{\rm{.}}{{\rm{I}}_1} + {{\rm{R}}_2}{\rm{.}}{{\rm{I}}_2}\) hay \(36{{\rm{I}}_1} + 90{{\rm{I}}_2} = 60\) \( \Rightarrow 6{{\rm{I}}_1} + 15{{\rm{I}}_2} = 10\).
Ta có hệ phương trình: \[\left\{ {\begin{array}{*{20}{c}}{{{\rm{I}}_1} - {{\rm{I}}_2} - {{\rm{I}}_3} = 0}\\{3{{\rm{I}}_2} - 2{{\rm{I}}_3} = 0}\\{6{{\rm{I}}_1} + 15{{\rm{I}}_2} = 10}\end{array}} \right.\]
Giải hệ phương trình, ta được \({{\rm{I}}_1} = \dfrac{5}{6}(\;{\rm{A}}),{{\rm{I}}_2} = \dfrac{1}{3}(\;{\rm{A}}),{{\rm{I}}_3} = \dfrac{1}{2}(\;{\rm{A}})\).
Ví dụ 3:
Ba tế bào \(A,B,C\) sau một số lần nguyên phân tạo ra 88 tế bào con. Biết số tế bào \(B\) tạo ra gấp đôi số tế bào \(A\) tạo ra. Số lần nguyên phân của tế bào \(B\) ít hơn số lần nguyên phân của tế bào \(C\) là hai lần. Tính số lần nguyên phân của mỗi tế bào, biết rằng một tế bào sau một lần nguyên phân sẽ tạo ra hai tế bào mới giống tế bào ban đầu.
Giải
Gọi \(x,y,z\) lần lượt là số lần nguyên phân của mỗi tế bào \(A,B,C(x,y,z \in \mathbb{N})\).
Tổng các tế bào con là 88 , ta có \({2^x} + {2^y} + {2^z} = 88\).
Số tế bào \(B\) tạo ra gấp đôi số tế bào \(A\) tạo ra, ta có \({2^y} = {2.2^x}\).
Số lần nguyên phân của tế bào \(B\) it hơn số lần nguyên phân của tế bào \(C\) là hai lần, ta có \(y + 2 = z\).
Từ đó, ta có hệ phương trình
\(\left\{ {\begin{array}{*{20}{l}}{{2^x} + {2^y} + {2^z} = 88}\\{{2^y} = {{2.2}^x}}\\{y + 2 = z}\end{array}{\rm{hay}}\left\{ {\begin{array}{*{20}{l}}{{2^x} + {2^y} + {2^z} = 88}\\{{{2.2}^x} - {2^y} = 0}\\{{2^{y + 2}} = {2^z}}\end{array}\quad {\rm{hay}}\left\{ {\begin{array}{*{20}{l}}{{2^x} + {2^y} + {2^z} = 88}\\{{{2.2}^x} - {2^y} = 0}\\{{{4.2}^y} - {2^z} = 0.}\end{array}} \right.} \right.} \right.\)
Đặt \(a = {2^x},b = {2^y},c = {2^z}\). Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{a + b + c = 88}\\{2a - b = 0}\\{4b - c = 0.}\end{array}} \right.\)
Sử dụng máy tính cầm tay giải hệ phương trình, ta được \(a = 8,b = 16,c = 64\).
Do đó \(x = 3,y = 4,z = 6\).
Vậy số lần nguyên phân của mỗi tế bào \(A,B,C\) lần lượt là \(3,4,6.\)
II. Ứng dụng trong kinh tế
1. Mô hình cân bằng thị trường hàng hoá có liên quan
Giả sử trên thị trường có \(n\) loại hàng hoá được mua và bán, đánh số lần lượt là hàng hoá \(1,2, \ldots ,n\). Ta nói \(n\) loại hàng hoá đó có liên quan nếu giá của một mặt hàng nào đó thay đổi thì nó không những ảnh hưởng tới lượng cung (kí hiệu là \({Q_S}\) ) và lượng cầu (kí hiệu là \({Q_{{D_i}}}\) ) của bản thân mặt hàng đó, mà nó còn ảnh hưởng tới giá và lượng cung, lượng cầu của các mặt hàng còn lại.
Như vậy, đối vối \(n\) loại hàng hoá có liên quan thì lượng cung \({Q_{{S_i}}}\) (hoặc lượng cầu \({Q_{{D_i}}}\) ) của mỗi loại hàng hoá là một đại lượng phụ thuộc vào \(n\) biến \({P_1},{P_2}, \ldots ,{P_n}\), trong đó \({P_1},{P_2}, \ldots ,{P_n}\) lần lượt là giá của hàng hoá \(1,2, \ldots ,n\).
Người ta thường biểu diễn sự phụ thuộc của lượng cung và lượng cầu vào giá của các hàng hoá bởi hàm cung và hàm cầu như sau:
\(\begin{array}{l}{Q_{{S_i}}} = {S_i}\left( {{P_1},{P_2}, \ldots ,{P_n}} \right),\\{Q_{{D_i}}} = {D_i}\left( {{P_1},{P_2}, \ldots ,{P_n}} \right)(1 \le i \le n)\end{array}\)
trong đó \({P_1},{P_2}, \ldots ,{P_n}\) lần lượt là giá của hàng hoá \(1,2, \ldots ,n\).
Mô hình cân bằng thị trường \(n\) loại hàng hoá có liên quan (cân bằng cung cầu) được xác định bởi hệ phương trình: \({Q_{{S_i}}} = {Q_{{D_i}}},1 \le i \le n\).
Giải hệ phương trình đó chúng ta tìm được bộ giá cân bằng thị trường: \(\bar P = \left( {\overline {{P_1}} ,\overline {{P_2}} , \ldots ,\overline {{P_n}} } \right)\).
Thay vào \({Q_{{S_i}}}\) (hoặc \({Q_D}\) ) chúng ta thu được bộ lượng cân bằng thị trường: \(\bar Q = \left( {\overline {{Q_1}} ,\overline {{Q_2}} , \ldots ,\overline {{Q_n}} } \right)\).
2. Mô hình cân bằng thu nhập quốc dân
Tổng thu nhập quốc dân, ki hiệu là \(Y\), thường được tính trên hai nguồn chủ yếu: Chi tiêu cố định của chính phủ, kí hiệu là \({G_0}\), và tiền của người dân (bao gồm đầu tư của các hộ gia đinh, kí hiệu là \({I_0}\), và tiêu dùng của các hộ gia đình, kí hiệu là \(C\) ). Ta nói thu nhập quốc dân là cân bằng nếu \(Y = C + {I_0} + {G_0}\).
Xét mô hình cân bằng thu nhập quốc dân có dạng hệ phương trình bậc nhất:
\(\left\{ {\begin{array}{*{20}{l}}{Y = C + {I_0} + {G_0}}\\{C = a(Y - T) + b}\\{T = \alpha Y}\end{array}} \right.\)
Trong đó: \(T\) là thuế, \(C = a(Y - T) + b\), các hằng số \(0 < a < 1,b > 0,0 < \alpha < 1\) được chọn trước (phụ thuộc vào sự lựa chọn mô hình của các nhà hoạch định chính sách).
