I. Tọa độ của vectơ
1. Tọa độ của một điểm
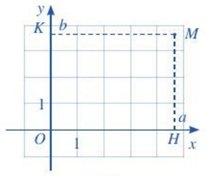
Để xác định toạ độ của một điểm \(M\) tuỳ ý trong mặt phẳng toạ độ $Oxy$, ta làm như sau:
- Từ \(M\) kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm \(H\) ứng với số \(a\). Số \(a\) là hoành độ của điểm \(M\).
- Từ \(M\) kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm \(K\) ứng với số \(b\). Số \(b\) là tung độ của điểm \(M\).
Cặp số \((a;b)\) là toạ độ của điểm \(M\) trong mặt phẳng toạ độ $Oxy$.
Ta kí hiệu là \(M(a;b)\).
2. Tọa độ của một vectơ
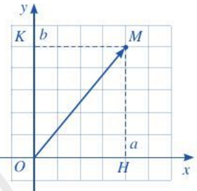
Tọa độ của điểm \(M\) được gọi là tọa độ của vectơ \(\overrightarrow {OM} \).
Nếu \(\overrightarrow {OM} \) có toạ độ \((a;b)\) thì ta viết \(\overrightarrow {OM} = (a;b)\).
Định lí:
Trong mặt phẳng toạ độ $Oxy$, nếu \(\vec u = (a;b)\) thì \(\vec u = a\vec i + b\vec j\). Ngược lại, nếu \(\vec u = a\vec i + b\vec j\) thì \(\vec u = (a;b)\).
3. Liên hệ giữa tọa độ của điểm và tọa độ của vectơ
Trong mặt phẳng tọa độ $O x y$, cho hai điểm \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\).
Ta có: \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)\).
II. Biểu thức tọa độ của các phép toán vectơ
1. Biểu thức tọa độ của phép cộng hai vectơ, phép trừ hai vectơ, phép nhân một số với một vectơ
Cho \(\vec u{\rm{\;}} = (x;y)\) ;\(\vec u'{\rm{\;}} = (x';y')\) và số thực . Khi đó ta có:
1) \(\vec u = \vec u' \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = x'}\\{y = y'}\end{array}} \right.\)
2) \(\vec u{\rm{\;}} \pm \vec v{\rm{\;}} = (x \pm x';y \pm y')\)
3) \(k.\vec u{\rm{\;}} = (kx;ky)\)
4) \(\vec u'\) cùng phương \(\vec u\)(\(\vec u{\rm{\;}} \ne \vec 0\)) khi và chỉ khi có số \(k\) sao cho \(\left\{ {\begin{array}{*{20}{l}}{x' = kx}\\{y' = ky}\end{array}} \right.\)
2. Tọa độ trung điểm đoạn thẳng và tọa độ trọng tâm tam giác
a)Cho hai điểm \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\). Nếu \(M\left( {{x_M};{y_M}} \right)\) là trung điểm đoạn thẳng $A B$ thì
\({x_M} = \dfrac{{{x_A} + {x_B}}}{2};{y_M} = \dfrac{{{y_A} + {y_B}}}{2}.\)
b) Cho tam giác $A B C$ có \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\). Nếu \(G\left( {{x_G};{y_G}} \right)\) là trọng tâm tam giác $ABC$ thì
\({x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3};{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}.\)
3. Biểu thức tọa độ của tích vô hướng
Nếu \(\vec u = \left( {{x_1};{y_1}} \right)\) và \(\vec v = \left( {{x_2};{y_2}} \right)\) thì \(\vec u \cdot \vec v = {x_1}{x_2} + {y_1}{y_2}\).
Nhận xét
a) Nếu \(\vec a = (x;y)\) thi \(|\vec a| = \sqrt {\vec a \cdot \vec a} = \sqrt {{x^2} + {y^2}} \).
b) Nếu \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\) thì \(AB = |\overrightarrow {AB} | = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \).
c) Với hai vectơ \(\vec u = \left( {{x_1};{y_1}} \right)\) và \(\vec v = \left( {{x_2};{y_2}} \right)\) khác \(\vec 0\), ta có:
\(\vec u\) và vuông góc với nhau khi và chỉ khi \({x_1}{x_2} + {y_1}{y_2} = 0\).
\(\cos (\vec u,\vec v) = \dfrac{{\vec u \cdot \vec v}}{{|\vec u| \cdot |\vec v|}} = \dfrac{{{x_1}{x_2} + {y_1}{y_2}}}{{\sqrt {x_1^2 + y_1^2} \cdot \sqrt {x_2^2 + y_2^2} }}.\)
III. Phương trình đường thẳng
1.Phương trình tham số của đường thẳng
Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu \(\overrightarrow u \ne \overrightarrow 0 \) và giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).
Chú ý:
Nếu \(\overrightarrow u \) là một vectơ chỉ phương của \(\Delta \) thì \(k\overrightarrow u \left( {k \ne 0} \right)\) cũng là một vectơ chỉ phương của \(\Delta \).
Phương trình tham số:
Hệ \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array}} \right.\)(với \({a^2} + {b^2} > 0,\,\,t \in R\)) trong đó \(t\) là tham số,
được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận\(\overrightarrow u = \left( {a;b} \right)\) làm vecto chỉ phương.
Nhận xét:
Cho \(t\) một giá trị cụ thể thì ta xác định được một điểm trên đường thẳng \(\Delta \) và ngược lại.
2.Phương trình tổng quát của đường thẳng
Vectơ \(\overrightarrow n \) được gọi là vectơ pháp tuyến của đường thẳng \(\Delta \) nếu \(\overrightarrow n \ne \overrightarrow 0 \) và giá của \(\overrightarrow n \) vuông góc với \(\Delta \).
Chú ý:
- Nếu \(\overrightarrow u \) là một vectơ pháp tuyến của \(\Delta \) thì \(k\overrightarrow u \left( {k \ne 0} \right)\) cũng là một vectơ pháp tuyến của \(\Delta \).
- Hai vectơ \(\overrightarrow n \left( {a;b} \right)\) và \(\left( { - b;a} \right)\) vuông góc với nhau nên nếu \(\overrightarrow n \) là vectơ pháp tuyến của đường thẳng \(\Delta \) thì \(\overrightarrow u \) là vectơ chỉ phương của đường thẳng đó và ngược lại.
Phương trình tổng quát:
Phương trình \(ax + {\rm{ }}by + {\rm{ }}c = 0\)(a và b không đồng thời bằng 0) được gọi là phương trình tổng quát của đường thẳng.
Nhận xét
- Đường thẳng A đi qua điểm \(M\left( {x;y} \right)\) và nhận \(\overrightarrow n \left( {a;b} \right)\) làm vectơ pháp tuyến có phương trình là:
\(a\left( {x - {x_0}} \right) + {\rm{ }}b\left( {y - {y_0}} \right) = 0 \Leftrightarrow ax + by + \left( { - ax - by} \right) = 0\)
- Mỗi phương trình \(ax + {\rm{ }}by + {\rm{ }}c = 0\) (a và b không đồng thời bằng 0) đều xác định một đường thẳng \(\Delta \) trên mặt phẳng toạ độ nhận một vectơ pháp tuyến là \(\overrightarrow n \left( {a;b} \right)\).
3.Liên hệ giữa đồ thị hàm số bậc nhất và đường thẳng
Đồ thị hàm bậc nhất \(y = kx + {y_0}\) là một đường thẳng có vectơ pháp tuyển \(\vec n = (k; - 1)\) và có phương trình tổng quát là \(kx - y + {y_0} = 0\). Đường thẳng này không vuông góc với \(Ox\) và \(Oy\).
Ngược lại, cho đường thẳng \(d\) có phương trình tổng quát \(ax + by + c = 0\) với \(a\) và \(b\) đều khác 0 , khi đó ta có thể viết: \(ax + by + c = 0 \Leftrightarrow y = - \dfrac{a}{b}x - \dfrac{c}{b} \Leftrightarrow y = kx + {y_0}\).
Như vậy d là đồ thị của hàm bậc nhất \(y = kx + {y_0}\) với hệ số góc \(k = - \dfrac{a}{b}\) và tung độ gốc \({y_0} = - \dfrac{c}{b}\)
IV. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
1.Vị trí tương đối của hai đường thẳng
Trên mặt phẳng toạ độ, xét hai đường thẳng
\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0.{\rm{ }}\)
Khi đó, toạ độ giao điểm của \({\Delta _1}\) và \({\Delta _2}\) là nghiệm của hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{{a_1}x + {b_1}y + {c_1} = 0}\\{{a_2}x + {b_2}y + {c_2} = 0.}\end{array}} \right.\)
\({\Delta _1}\) cắt \({\Delta _2}\) tại \(M\left( {{x_0};{y_0}} \right) \Leftrightarrow \) hệ \((*)\) có nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\).
\({\Delta _1}\) song song với \({\Delta _2} \Leftrightarrow \) hệ \((*)\) vô nghiệm.
\({\Delta _1}\) trùng \({\Delta _2} \Leftrightarrow \) hệ \((*)\) có vô số nghiệm.
2.Góc giữa hai đường thẳng
Hai đường thẳng cắt nhau tạo thành bốn góc, số đo của góc không tù được gọi là số đo góc giữa hai đường thẳng.
Cho hai đường thẳng
\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0,\)
với các vectơ pháp tuyến \(\overrightarrow {{n_1}} \left( {{a_1};{b_1}} \right)\) và \(\overrightarrow {{n_2}} \left( {{a_2};{b_2}} \right)\) tương ứng. Khi đó, góc \(\varphi \) giữa hai đường thẳng đó được xác định thông qua công thức
\(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \dfrac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \dfrac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \cdot \sqrt {a_2^2 + b_2^2} }}.\)
3.Khoảng cách từ một điểm đến một đường thẳng
Cho điểm \(M\left( {{x_0};{y_0}} \right)\) và đường thẳng \(\Delta :ax + by + c = 0\). Khoảng cách từ điểm \(M\) đến đường thẳng \(\Delta \), kí hiệu là \(d(M,\Delta )\), được tính bởi công thức
\(d(M,\Delta ) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\)
V. Phương trình đường tròn
1. Phương trình đường tròn
Phương trình đường tròn tâm \(I\left( {a;b} \right)\) bán kính R là:
\({(x - a)^2} + {(y - b)^2} = {R^2}\)
Phương trình đường tròn ở dạng trên thường được gọi là phương trình chính tắc của đường tròn.
Nhận xét: Ta có thể viết phương trình \({\left( {x{\rm{ }} - a} \right)^2} + {\left( {y - b} \right)^2} = {\rm{ }}{R^2}\) của đường tròn tâm I(a; b) bán kính R về phương trình có dạng là \({x^2} + {y^2}--2ax--2by + c = 0\left( {c = {a^2} + {b^2} - R} \right)\). Dạng đó thường được gọi là phương trình tổng quát của đường tròn.
Ngược lại, phương trình \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình của đường tròn (C) khi và chỉ khi \(a + b - c > 0\). Khi đó đường tròn (C) có tâm \(I\left( {a,{\rm{ }}b} \right)\) và bán kính
2. Phương trình tiếp tuyến của đường tròn
Đường thẳng \({M_0}t\) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và có vectơ pháp tuyến
\(\overrightarrow {I{M_0}} = \left( {{x_0} - a;{y_0} - b} \right).\)\(\)
Phương trình tiếp tuyến \({M_0}t\) là:
\(\left( {{x_0} - a} \right)\left( {x - {x_0}} \right) + \left( {{y_0} - b} \right)\left( {y - {y_0}} \right) = 0.{\rm{ }}\)
VI. Ba đường conic
1.Đường Elip
Cho hai điểm cố định \({F_1},\,{F_2}\) và một độ dài không đổi \(2a\) lớn hơn \({F_1}{F_2}\). Elip (E) là tập hợp các điểm M trong mặt phẳng sao cho \({F_1}M + {F_2}M = 2a.\)
Các điểm \({F_1}\) và \({F_2}\) gọi là các tiêu điểm của elip.
Độ dài \({F_1}{F_2} = 2c\) gọi là tiêu cự của elip (a > c).
Phương trình chính tắc của elip:
Trong đó \(b = \sqrt {{a^2} - {c^2}} \)
Trong mặt phẳng toạ độ Oxy, elip có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó, thì có phương trình
\(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{b} = 1\) (1)
Ngược lại, mỗi phương trình có dạng (1), với a >b>0, đều là phương trình của elip có hai tiêu điểm \({F_1}\left( { - \sqrt {{a^2} - {b^2}} ;0} \right),\,\,\,{F_1}\left( {\sqrt {{a^2} - {b^2}} ;0} \right)\), tiêu cự \(2c = 2\sqrt {{a^2} - {b^2}} \) và tổng các khoảng cách từ mỗi điểm thuộc elip đó tới hai tiêu điểm bằng 2a.
Phương trình (2) được gọi là phương trình chính tắc của elip tương ứng.
2.Đường Hypebol
Cho hai điểm phân biệt cố định \({F_1}\) và \({F_2}\). Đặt \({F_1}{F_2} = 2c\). Cho số thực dương a nhỏ hơn c.
Tập hợp các điểm M sao cho \(\left| {M{F_1}--M{F_2}} \right| = 2a\) được gọi là đường hypebol (hay hypebol). Hai điểm \({F_1}\),\({F_2}\) được gọi là hai tiêu điểm và \({F_1}{F_2} = 2c\) được gọi là tiêu cự của hypebol đó.
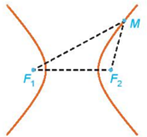
Chú ý: Hypebol có hai nhánh, một nhánh gồm những điểm M thoả mãn \(M{F_1}--M{F_2} = 2a\) và nhánh còn lại gồm những điểm M thoả mãn \(M{F_1}--M{F_2} = - 2a\)
Phương trình chính tắc của hypebol:
Trong mặt phẳng toạ độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho \(O\) là trung điểm của đoạn nối hai tiêu điểm đó, thì có phương trình
\(\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1{\rm{, }}\)với \(a,b > 0.{\rm{ }}\) (2)
Ngược lại, mỗi phương trình (2), với \(a,b > 0\), đều là phương trình của hypebol có hai tiêu điểm \({F_1}\left( { - \sqrt {{a^2} + {b^2}} ;0} \right),{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right)\), tiêu cự \(2c = 2\sqrt {{a^2} + {b^2}} \) và giá trị tuyệt đối của hiệu các khoảng cách từ một điểm thuộc hypebol đến hai tiêu điểm bằng \(2a\).
Phương trình (2) được gọi là phương trình chính tắc của hypebol tương ứng.
3.Đường Parabol
Cho một điểm F cố định và một đường thẳng \(\Delta \) cố định không đi qua F. Tập hợp các điểm M cách đều F và \(\Delta \) được gọi là đường parabol (hay parabol). Điểm F được gọi là tiêu điểm, \(\Delta \) được gọi là đường chuẩn, khoảng cách từ F đến \(\Delta \) được gọi là tham số tiêu của parabol đó.
Xét \((P)\) là một parabol với tiêu điểm \(F\), đường chuẩn \(\Delta \). Gọi H là hình chiếu vuông góc của \(F\) trên \(\Delta \). Khi đó, trong hệ trục toạ độ Oxy với gốc \(O\) là trung điểm của HF, tia Ox trùng tia OF, parabol \((P)\) có phương trình
\({y^2} = 2px\), với \(p > 0\) (3)
Phương trình (3) được gọi là phương trình chính tắc của parabol \((P)\).
Ngược lại, mỗi phương trình dạng (3), với \(p > 0\), là phương trình chính tắc của parabol có tiêu điểm \(F\left( {\dfrac{p}{2};0} \right)\) và đường chuẩn \(\Delta :x = - \dfrac{p}{2}\).
\(\left( {\dfrac{{11}}{4}; - \dfrac{{\sqrt {11} }}{2}} \right)\).
