I. Định nghĩa tổ hợp
Cho tập hợp A gồm n phần tử và một số nguyên k với \(1 < k \le n\).
Mỗi tập con gồm k phần tử được lấy ra từ n phần tử của A được gọi là một tổ hợp chập k của n phần tử đó.
Ví dụ: Bạn Quân có 4 chiếc áo sơ mi khác màu là áo vàng, áo xanh, áo trắng và áo nâu.
Bạn muốn chọn 2 chiếc áo để mặc khi đi du lịch. Viết các tổ hợp chập 2 của 4 chiếc áo.
Giải
Các tổ hợp chập 2 của 4 chiếc áo là:
{áo vàng; áo xanh}, {áo vàng; áo trắng}, {áo vàng; áo nâu},
{áo xanh; áo trắng}, {áo xanh; áo nâu}, {áo trắng; áo nâu}.
II. Số các tổ hợp
Số các tổ hợp chập \(k\) của \(n\) phần tử \(\left( {1 \le k \le n} \right)\) bằng
\(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\)
Chú ý:
+ Quy ước \(C_n^0 = 1\)
+ \(C_n^k = \dfrac{{A_n^k}}{{k!}}\)
- Chỉnh hợp và tổ hợp có điểm giống nhau là đều chọn một số phần tử trong một tập hợp, nhưng khác nhau ở chỗ, chỉnh hợp là chọn có xếp thứ tự, còn tổ hợp là chọn không xếp thứ tự.
Ví dụ: Có 7 bạn học sinh muốn chơi cờ cá ngựa, nhưng mỗi ván chỉ có 4 người chơi. Hỏi có bao nhiêu cách chọn 4 bạn chơi cờ cá ngựa?
Giải
Mỗi cách chọn 4 bạn trong 7 bạn học sinh là một tổ hợp chập 4 của 7.
Vậy số cách chọn 4 bạn chơi cờ cá ngựa là: \(C_7^4 = \dfrac{{7!}}{{4!3!}} = 35\)
III. Tính chất tổ hợp chập k của n phần tử Ta có hai đẳng thức sau:
Ta có hai đẳng thức sau:
+\(C_n^k = C_n^{n - k}\left( {0 \le k \le n} \right)\)
+\(C_{n - 1}^{k - 1} + C_{n - 1}^k = C_n^k\left( {1 \le k < n} \right)\)
Ví dụ:
a) \(C_9^4 = C_9^5\)
b) \(C_8^3 + C_8^4 = C_9^4\)
IV. Tính số các hoán vị, chỉnh hợp, tổ hợp bằng máy tính cầm tay
1.Hoán vị
Để tính \({P_8} = 8!\), ta ấn liên tiếp các phím:
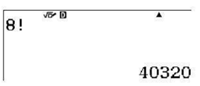
Ta được kết quả là 40 320
2.Chỉnh hợp
Để tính \(A_{12}^5\), ta ấn liên tiếp các phím:
Ta nhận được kết quả là 95 040.
3.Tổ hợp
Để tính \(C_{20}^{11}\), ta ấn liên tiếp các phím:
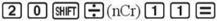
Ta nhận được kết quả là 167 960.
