I. Tính đối xứng của parabol
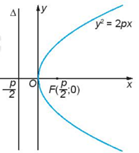
Ta đã biết parabol (P) với phương trình chính tắc \({y^2} = 2px\) có:
- Tiêu điểm \(F\left( {\dfrac{p}{2};0} \right)\) và có đường chuẩn \(\Delta :x = - \dfrac{p}{2}\)
- Parabol (P) nhận Ox làm trục đối xứng
- Giao điểm của parabol (P) và trục đối xứng của nó gọi là đỉnh của parabol.
Chú ý:
a) Với mọi điểm \(M\left( {x;y} \right)\) thuộc parabol \(\left( P \right):{y^2} = 2px\) (với \(p > 0\)) ta đều có \(x \ge 0\), suy ra (P) thuộc nửa mặt phẳng toạ độ có \(x \ge 0\).
b) Vì \( - \dfrac{p}{2} < 0\) nên đường chuẩn của parabol không có điểm chung với parabol đó.
c) Nếu điểm \(M\left( {x;y} \right)\) nằm trên parabol (P) thì điểm \(M'\left( {{x_0}; - {y_0}} \right)\) cũng nằm trên parabol (P).
Khoảng cách từ tiêu điểm đến đường chuẩn gọi là tham số tiêu của parabol.
Đường parabol chỉ có một trục đối xứng, một đỉnh và không có tâm đối xứng.
II. Bán kính qua tiêu và tâm sai của parabol
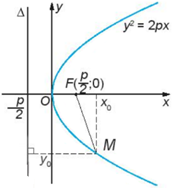
Cho parabol có phương trình chính tắc \({y^2} = 2px,{\rm{ }}p > 0\). Khi đó:
- Với điểm \(M\left( {x;y} \right)\) thuộc parabol, đoạn thẳng MF được gọi là bán kính qua tiêu của M và có độ dài \(MF = x + \dfrac{p}{2}\)
- Với mọi điểm \(M\left( {x;y} \right)\) thuộc parabol, tỉ số \(\dfrac{{MF}}{{d\left( {M,\Delta } \right)}}\) luôn bằng 1. Ta nói parabol có tâm sai bằng 1.
Ví dụ:
Tính bán kính qua tiêu của điểm \(M\left( {1;2} \right)\) trên parabol \(\left( P \right):{y^2} = 4x\)
Giải
Ta có \(2p = 4 \Rightarrow p = 2\)
Độ dài bán kính qua tiêu của điểm \(M\left( {1;2} \right)\) là:
\(FM = x + \dfrac{p}{2} = 1 + \dfrac{2}{2} = 2\)
III. Cách vẽ đường parabol
Để vẽ parabol \({y^2} = 2px\left( {p > 0} \right),\) ta có thể làm như sau:
- Xác định đỉnh và một số điểm cụ thể.
- Vẽ parabol đi qua những điểm cụ thể đã chọn, tiếp xúc với trục tung tại đỉnh \(O\left( {0{\rm{ }};0} \right)\) và nhận trục hoành làm trục đối xứng.
